 , and corresponding eigenvectors ,
, and corresponding eigenvectors , 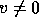 , such that
, such that
The nonsymmetric eigenvalue problem is to find the eigenvalues ,
 , and corresponding eigenvectors ,
, and corresponding eigenvectors , 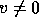 , such that
, such that

A real matrix A may have complex eigenvalues, occurring as complex conjugate
pairs. More precisely, the vector v is called a right
eigenvector of A, and a vector 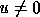 satisfying
satisfying

is called a left eigenvector of A.
This problem can be solved via the Schur factorization of A, defined in the real case as

where Z is an orthogonal matrix and T is an upper quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks, the 2-by-2 blocks corresponding to complex conjugate pairs of eigenvalues of A. In the complex case the Schur factorization is

where Z is unitary and T is a complex upper triangular matrix.
The columns of Z are called the Schur vectors . For each k (1 < = k < = n) , the first k columns of Z form an orthonormal basis for the invariant subspace corresponding to the first k eigenvalues on the diagonal of T. Because this basis is orthonormal, it is preferable in many applications to compute Schur vectors rather than eigenvectors. It is possible to order the Schur factorization so that any desired set of k eigenvalues occupy the k leading positions on the diagonal of T.
Two pairs of drivers are provided, one pair focusing on the Schur factorization, and the other pair on the eigenvalues and eigenvectors as shown in Table 2.5: