




Next: Local Storage Scheme for
Up: In-Core Narrow Band and
Previous: The Block Column and
The one-dimensional distribution scheme
is a mapping of a set of blocks onto
the processes. The previous section
informally described this mapping as
well as some of its properties. To
be complete, we shall describe
the precise mapping that associates
to a matrix entry identified by its
global indexes the coordinates of
the process that owns it and its
local position within that process's
memory.
Suppose we have a two dimensional
array A of size 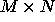 to
be distributed on a
to
be distributed on a 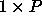 process grid in a block-column
fashion. By convention, the array
columns are numbered 1 through
N and the processes are numbered
0 through P-1. First, the array
is divided into contiguous blocks
of NB columns with
process grid in a block-column
fashion. By convention, the array
columns are numbered 1 through
N and the processes are numbered
0 through P-1. First, the array
is divided into contiguous blocks
of NB columns with 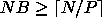 . When NB does not
divide N evenly, the last block
of columns will only contain
. When NB does not
divide N evenly, the last block
of columns will only contain
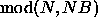 columns instead
of NB. By convention, these blocks
are numbered starting from zero and
dealt out to the processes. In other
words, if we assume that the process
0 receives the first block, the
columns instead
of NB. By convention, these blocks
are numbered starting from zero and
dealt out to the processes. In other
words, if we assume that the process
0 receives the first block, the
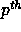 block is assigned to the
process of coordinate (0,p).
The mapping of a column of the
array globally indexed by J is
defined by the following analytical
equation:
block is assigned to the
process of coordinate (0,p).
The mapping of a column of the
array globally indexed by J is
defined by the following analytical
equation:

where J is a global column index
in the array, p is the column
coordinate of the process owning
that column, and finally x is
the column coordinate within that
block of columns where the global
array column of index J is to be
found. It is then fairly easy to
establish the analytical relationship
between these variables. One obtains:
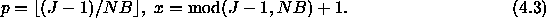
These equations allow to determine
the local information, i.e. the
local index x as well as the
process column coordinate p
corresponding to a global column
identified by its global index J
and conversely. Table 4.9
illustrates this mapping layout when
P=2 and N=16 and NB=8. At most
one block is assigned to each process.

Table 4.9: One-dimensional block-column mapping example for P=2 and N=16
This example of the one-dimensional
block-column distribution mapping
can be expressed in HPF
by using the following statements:
REAL :: A( M, N )
!HPF$ PROCESSORS PROC( 1, P )
!HPF$ DISTRIBUTE A( *, BLOCK( NB ) ) ONTO PROC
A similar example of block-row
distribution
can easily be constructed. For
an 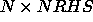 array B,
such an example can be expressed
in HPF by
using the following statements:
array B,
such an example can be expressed
in HPF by
using the following statements:
REAL :: B( N, NRHS )
!HPF$ PROCESSORS PROC( P, 1 )
!HPF$ DISTRIBUTE B( BLOCK( NB ), * ) ONTO PROC
There is in fact no real
reason to always deal out
the blocks starting with
the process 0. In fact,
it is sometimes useful to
start the data distribution
with the process of arbitrary
coordinate SRC, in which case
Equation 4.3
becomes:
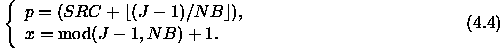
Table 4.10
illustrates Equation 4.4
for the block-cyclic layout when 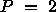 ,
,
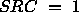 ,
, 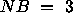 and
and 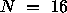 .
.

Table 4.10: One-dimensional block-column mapping for P=2, SRC=1,
N=16 and NB=8
This example of the
one-dimensional block-column
distribution mapping can be
expressed in HPF
by using the following statements:
REAL :: A( M, N )
!HPF$ PROCESSORS PROC( 1, P )
!HPF$ TEMPLATE T( M, N + P*NB )
!HPF$ DISTRIBUTE T( *, BLOCK( NB ) ) ONTO PROC
!HPF$ ALIGN A( I, J ) WITH T( I, SRC*NB + J )
A similar example of block-row
distribution
can easily be constructed. For
an 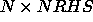 array B,
such an example can be expressed
in HPF by
using the following statements:
array B,
such an example can be expressed
in HPF by
using the following statements:
REAL :: B( N, NRHS )
!HPF$ PROCESSORS PROC( P, 1 )
!HPF$ TEMPLATE T( N + P*NB, NRHS )
!HPF$ DISTRIBUTE T( BLOCK( NB ), * ) ONTO PROC
!HPF$ ALIGN A( I, J ) WITH T( SRC*NB + I, J )
In ScaLAPACK, the local storage
convention of the one-dimensional
block distributed matrix in every
process's memory is assumed to be
Fortran-like, that is, ``column major'' .
Determining the number of rows or columns
of a global band matrix that a specific
process receives is an essential task for
the user. The notation LOC () is
used for block-row distributions and
LOC
() is
used for block-row distributions and
LOC () is used for block-column
distributions. These local quantities
occur throughout the leading comments
of the source code, and are reflected
in the sample argument description in
section 4.4.7.
() is used for block-column
distributions. These local quantities
occur throughout the leading comments
of the source code, and are reflected
in the sample argument description in
section 4.4.7.
For block distribution, a matrix can be
distributed unevenly. More specifically,
one process in the process grid can receive
an array that is smaller than other processes.
It is also possible that some processes
receive no data. For further information
on one-dimensional block-column or
block-row data distribution, please
refer to section 4.4.1.
Block-Column Distribution: LOC (N_A)
denotes the number of columns that a process would
receive if N_A columns of a matrix is distributed
over
(N_A)
denotes the number of columns that a process would
receive if N_A columns of a matrix is distributed
over 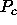 columns of its process row.
columns of its process row.
For example, let us assume that the coefficient
matrix A is band symmetric of order N and has
been block-column distributed on a 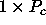 process grid.
process grid.
In the ideal case where the matrix is evenly
distributed to all processes in the process
grid, 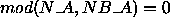 and
and 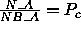 .
Thus, each process receives a block of size
.
Thus, each process receives a block of size 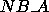 of the matrix A. Therefore,
of the matrix A. Therefore,
LOC (N_A) = NB_A.
(N_A) = NB_A.
However, if 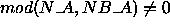 ,
at least one of the processes in the
process grid will receive a block of
size smaller than
,
at least one of the processes in the
process grid will receive a block of
size smaller than 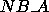 . Thus,
. Thus,
if ( 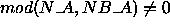 and
and 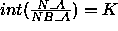 ) then
) then
processes (0,0), ... , (0,K-1) receive
LOC (N_A) = NB_A
(N_A) = NB_A
and process (0,K) receives
LOC (N_A) = N_A - K
(N_A) = N_A - K  NB_A.
NB_A.
if  then processes
then processes 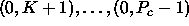 do
not receive any data.
do
not receive any data.
end if
Block-Row Distribution: LOC (M_B)
denotes the number of rows that a process would
receive if M_B rows of a matrix is distributed
over
(M_B)
denotes the number of rows that a process would
receive if M_B rows of a matrix is distributed
over 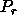 rows of its process column.
rows of its process column.
Let us assume that the N-by-NRHS right-hand-side
matrix B has been block-row distributed on a
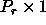 process grid.
process grid.
In the ideal case where the matrix is evenly
distributed to all processes in the process grid,
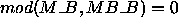 and
and 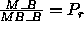 .
Thus, each process receives a block of size
.
Thus, each process receives a block of size 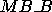 of the matrix B. Therefore,
of the matrix B. Therefore,
LOC (M_B) = MB_B.
(M_B) = MB_B.
However, if 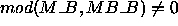 , then at
least one of the processes in the process grid
will receive a block of size smaller than
, then at
least one of the processes in the process grid
will receive a block of size smaller than 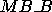 .
Thus,
.
Thus,
if ( 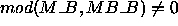 and
and 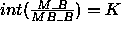 ) then
) then
processes t#tex2html_wrap_inline15295# receive
LOC (M_B) = MB_B
(M_B) = MB_B
and process (K,0) receives
LOC (M_B) = M_B - K
(M_B) = M_B - K  MB_B.
MB_B.
if  then processes
then processes 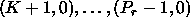 do
not receive any data.
do
not receive any data.
end if





Next: Local Storage Scheme for
Up: In-Core Narrow Band and
Previous: The Block Column and
Susan Blackford
Tue May 13 09:21:01 EDT 1997

