Argument Descriptions for Band and Tridiagonal Routines

           

All ScaLAPACK narrow band and tridiagonal routines assume that the global matrices are distributed in a one-dimensional block data distribution. Thus, each process has at most one block of data. With selective choices for the block size NB_ and the order N_ of the global matrix, it is possible that some processes in the process grid may not receive any data, or the last process receiving data will receive a smaller block of data than the other processes.

For further information on one-dimensional block-column or block-row data distribution, please refer to section 4.4.1.

The description of a block-column distributed band matrix consists of (N, A, JA, DESCA)

• the order N of the band matrix operand,
• a pointer to the local array containing the entire global array (A, for example),
• the column index, JA, of the global array, and
• the array descriptor, DESCA, of the global array.

The description of a block-row distributed right-hand-side matrix consists of (NRHS, B, IB, DESCB)

• the number of right-hand-side vectors NRHS in the matrix,
• a pointer to the local array containing the entire global array (B, for example),
• the row index, IB, of the global array, and
• the array descriptor, DESCB, for the global array.

The description of a block-distributed diagonally dominant-like tridiagonal matrix consists of (N, DL, D, DU, JA, DESCA)

• the order N of the tridiagonal matrix operand,
• pointer to the local arrays, (DL, D, DU, for example),
• the column index, JA, of the global array, and
• the array descriptor, DESCA, for the global array.

The description of a block-distributed symmetric positive definite tridiagonal matrix consists of (N, D, E, JA, DESCA)

• the order N of the tridiagonal matrix operand,
• pointer to the local arrays, (D, E, for example),
• the column index, JA, of the global array,
• the array descriptor, DESCA, for the global array.

The name of the row or column index for the global array has the form I<array_name>  or J<array_name> , respectively. The array descriptor has a name of the form DESC<array_name> .    The length of the array descriptor is specified by DLEN_ and varies according to the descriptor type DTYPE_.

Included in the leading comments of each subroutine (immediately preceding the Argument section), is a brief note describing the array descriptor    and some commonly used expressions in calculating workspace.

The style of the argument  descriptions for symmetric positive definite narrow band routines (PxPByyy) and diagonally dominant-like narrow band routines (PxDByyy) is illustrated by the following example:

N
(global input) INTEGER
The number of rows and columns of the matrix A(JA:JA+N-1,JA:JA+N-1) on which to be operated. N 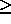0.
NRHS
(global input) INTEGER
The number of right hand sides, i.e., the number of columns of the matrix B(IB:IB+N-1,*). NRHS 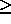0.
A
(local input/local output) REAL pointer into the local memory to an array of local dimension (LLD_A, LOC(JA+N-1))
On entry, the local part of the N-by-N global symmetric band matrix A(JA:JA+N-1,JA:JA+N-1).
JA
(global input) INTEGER
The column index of the global matrix A.
DESCA
(global and local input) INTEGER array of dimension DLEN_
The array descriptor for the global matrix A.
B
(local input/local output) REAL array, dimension (LLD_B, NRHS)
On entry, the local part of the N-by-NRHS right-hand-side matrix.
IB
(global input) INTEGER
The row index of the global matrix B.
DESCB
(global and local input) INTEGER array of dimension DLEN_
The array descriptor for the global matrix B.

The style of the argument  descriptions for diagonally dominant-like tridiagonal routines (PxDTyyy) is illustrated by the following example:

N
(global input) INTEGER
The number of rows and columns of the matrix A(JA:JA+N-1,JA:JA+N-1) on which to be operated. N 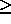0.
NRHS
(global input) INTEGER
The number of right hand sides, i.e., the number of columns of the matrix B(IB:IB+N-1,*). NRHS 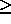0.
DL
(local input/local output) REAL pointer into the local memory to an array of local dimension (LOC(JA+N-1))
On entry, the local part of the subdiagonal entries of the global tridiagonal matrix A(JA:JA+N-1,JA:JA+N-1).
D
(local input/local output) REAL pointer into the local memory to an array of local dimension (LOC(JA+N-1))
On entry, the local part of the diagonal entries of the global tridiagonal matrix A(JA:JA+N-1,JA:JA+N-1).
DU
(local input/local output) REAL pointer into the local memory to an array of local dimension (LOC(JA+N-1))
On entry, the local part of the superdiagonal entries of the global tridiagonal matrix A(JA:JA+N-1,JA:JA+N-1).
JA
(global input) INTEGER
The column index of the global matrix A.
DESCA
(global and local input) INTEGER array of dimension DLEN_
The array descriptor for the global matrix A.
B
(local input/local output) REAL array, dimension (LLD_B, NRHS)
On entry, the local part of the N-by-NRHS right-hand-side matrix.
IB
(global input) INTEGER
The row index of the global matrix B.
DESCB
(global and local input) INTEGER array of dimension DLEN_
The array descriptor for the global matrix B.

The style of the argument  descriptions for symmetric positive definite tridiagonal routines (PxPTyyy) is illustrated by the following example:

N
(global input) INTEGER
The number of rows and columns of the matrix A(JA:JA+N-1,JA:JA+N-1) on which to be operated. N 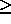0.
NRHS
(global input) INTEGER
The number of right hand sides, i.e., the number of columns of the matrix B(IB:IB+N-1,*). NRHS 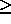0.
D
(local input/local output) REAL pointer into the local memory to an array of local dimension (LOC(JA+N-1))
On entry, the local part of the diagonal entries of the global tridiagonal matrix A(JA:JA+N-1,JA:JA+N-1).
E
(local input/local output) REAL pointer into the local memory to an array of local dimension (LOC(JA+N-1))
On entry, the local part of the off-diagonal entries of the global tridiagonal matrix A(JA:JA+N-1,JA:JA+N-1).
JA
(global input) INTEGER
The column index of the global matrix A.
DESCA
(global and local input) INTEGER array of dimension DLEN_
The array descriptor for the global matrix A.
B
(local input/local output) REAL array, dimension (LLD_B, NRHS)
On entry, the local part of the N-by-NRHS right-hand-side matrix.
IB
(global input) INTEGER
The row index of the global matrix B.
DESCB
(global and local input) INTEGER array of dimension DLEN_
The array descriptor for the global matrix B.

The description of each argument contains the following information:

• A classification of the argument as (local input), (global and local input), (local input/local output), (global input), (local output), (global output), (global input/global output), (local or global input) (local workspace), or (local workspace/local output).
• The type of the argument;
• For an array, its dimension(s).

  These dimensions are often expressed in terms of LOC() and LOC() calculations. For further details, please refer to section 4.4.2.

• A specification of the value(s) that must be supplied for the argument (if it is an input argument), or of the value(s) returned by the routine (if it is an output argument), or both (if it is an input/output argument). In the last case, the two parts of the description are introduced by the phrases ``On entry'' and ``On exit''.
• For a scalar input argument, any constraints that the supplied values must satisfy (such as ``N 0'' in the example above).