The linear least squares (LLS) problem is:
where A is an m-by-n matrix, b is a given m element vector
and x is the n element solution vector.
In the most usual case, 
and 
.
In this case the
solution to problem (3.1) is unique.
The problem is also
referred to as finding a least squares solution to an
overdetermined system of linear equations.
When m < n and 
, there are an infinite number
of solutions x
that exactly satisfy b-Ax=0. In this case it is often useful to find
the unique solution x that minimizes 
,
and the problem
is referred to as finding a minimum norm solution to an
underdetermined system of linear equations.
The driver routine PxGELS
solves problem (3.1) on the assumption that
-- in other words, A has full rank --
finding a least squares solution of an overdetermined system
when m > n, and a minimum norm solution of an underdetermined system
when m < n.
PxGELS uses a QR or LQ
factorization of A and also allows A to be
replaced by 
in the statement of the problem (or by 
if A is
complex).
In the general case when we may have
-- in other words,
A may be rank-deficient --
we seek the minimum norm least squares solution x
that minimizes both and 
.
The LLS driver routines are listed in table 3.3.
All routines allow several right-hand-side vectors b and corresponding
solutions x to be handled in a single call, storing these vectors as columns
of matrices B and X, respectively.
Note, however, that equation 3.1 is solved for
each right-hand-side vector independently; this is not the same as
finding a matrix X that minimizes 
.
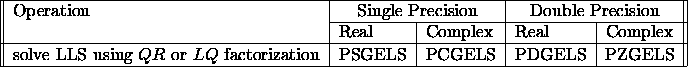
Table 3.3: Driver routines for linear least squares problems