




Next: Linear Least Squares Problems
Up: Driver Routines
Previous: Driver Routines
Two types of driver routines are provided for solving systems of linear
equations :
Both types of driver routines can handle multiple right-hand sides
(the columns of B).
Different driver routines are provided to take advantage of special
properties or storage schemes of the matrix A, as shown in
table 3.2.
These driver routines cover all the functionality of the computational
routines for linear systems , except matrix
inversion . It is seldom
necessary to compute the inverse of a matrix explicitly, and such computation
is certainly not recommended as a means of solving linear systems.
At present, only simple drivers (name ending -SV) are provided for
systems involving band and tridiagonal matrices.
It is important to note that in the banded and tridiagonal factorizations
(PxDBTRF, PxDTTRF, PxGBTRF, PxPBTRF, and PxPTTRF) used within these
drivers, the resulting
factorization is not the same factorization as returned from
LAPACK. Additional permutations are performed on the matrix for the
sake of parallelism. Further details of the algorithmic implementations
can be found in [32].
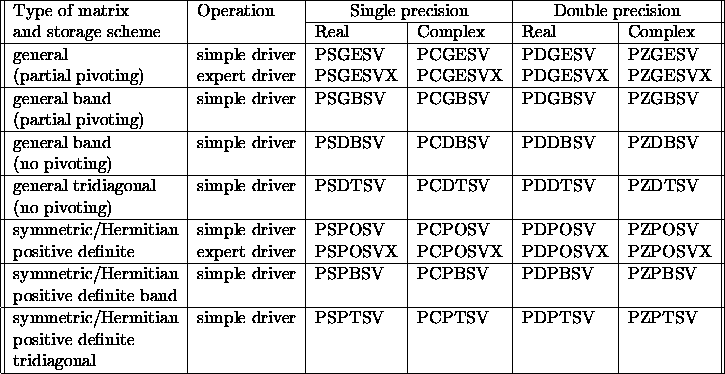
Table 3.2: Driver routines for linear equations





Next: Linear Least Squares Problems
Up: Driver Routines
Previous: Driver Routines
Susan Blackford
Tue May 13 09:21:01 EDT 1997
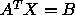 or
or 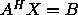 (unless A is symmetric or Hermitian);
(unless A is symmetric or Hermitian);
