




Next: Inverse Iteration
Up: Single- and Multiple-Vector Iterations
Previous: Single- and Multiple-Vector Iterations
Contents
Index
The simplest eigenvalue problem is to compute just the dominating
eigenvalue along with its eigenvector.
The power method presented in Algorithm 4.1
is the simplest iterative
method for this task. Under mild assumptions it finds the
eigenvalue of  which has the largest absolute value, and a
corresponding eigenvector.
which has the largest absolute value, and a
corresponding eigenvector.

Let 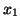 be the eigenvector corresponding to
be the eigenvector corresponding to
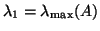 . The angle
. The angle 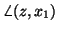 between
between 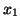 and
and 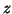 is defined by the relation
is defined by the relation
If the starting vector
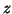 and the eigenvector
and the eigenvector 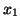 are perpendicular to each other, then
are perpendicular to each other, then
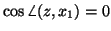 . In this case the power method does not converge
in exact arithmetic.
On the other hand, if
. In this case the power method does not converge
in exact arithmetic.
On the other hand, if
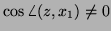 , the power method
generates a sequence of vectors that become increasingly
parallel to
, the power method
generates a sequence of vectors that become increasingly
parallel to 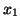 . This condition on
. This condition on 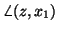 is true with
very high probability if
is true with
very high probability if 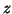 is chosen at random.
is chosen at random.
The convergence rate of the power method depends on
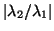 , where
, where 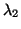 is the second largest
eigenvalue of
is the second largest
eigenvalue of  in magnitude.
This ratio is generally
smaller than
in magnitude.
This ratio is generally
smaller than 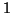 , allowing adequate convergence. But there
are cases where this ratio can be very close to
, allowing adequate convergence. But there
are cases where this ratio can be very close to 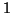 , causing very
slow convergence. For detailed discussions on the power
method, see Demmel [114, Chap. 4], Golub and Van
Loan [198], and Parlett [353].
, causing very
slow convergence. For detailed discussions on the power
method, see Demmel [114, Chap. 4], Golub and Van
Loan [198], and Parlett [353].





Next: Inverse Iteration
Up: Single- and Multiple-Vector Iterations
Previous: Single- and Multiple-Vector Iterations
Contents
Index
Susan Blackford
2000-11-20

![]() be the eigenvector corresponding to
be the eigenvector corresponding to
![]() . The angle
. The angle ![]() between
between ![]() and
and ![]() is defined by the relation
is defined by the relation
![]() , where
, where ![]() is the second largest
eigenvalue of
is the second largest
eigenvalue of ![]() in magnitude.
This ratio is generally
smaller than
in magnitude.
This ratio is generally
smaller than ![]() , allowing adequate convergence. But there
are cases where this ratio can be very close to
, allowing adequate convergence. But there
are cases where this ratio can be very close to ![]() , causing very
slow convergence. For detailed discussions on the power
method, see Demmel [114, Chap. 4], Golub and Van
Loan [198], and Parlett [353].
, causing very
slow convergence. For detailed discussions on the power
method, see Demmel [114, Chap. 4], Golub and Van
Loan [198], and Parlett [353].