




Next: Harmonic Ritz Values.
Up: Basic Ideas Y. Saad
Previous: Orthogonal Projection Methods.
Contents
Index
Oblique Projection Methods.
In an oblique projection method we are given two subspaces  and
and 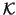 and
seek an approximation
and
seek an approximation 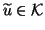 and an element
and an element
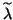 of
of 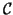 that satisfy the Petrov-Galerkin condition,
that satisfy the Petrov-Galerkin condition,
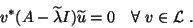 |
(12) |
The subspace 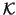 will be referred to as the right subspace and
will be referred to as the right subspace and
 as the left subspace.
A procedure similar to the Rayleigh-Ritz procedure can be devised, and
this can be conveniently described in matrix form by
expressing the approximate eigenvector
as the left subspace.
A procedure similar to the Rayleigh-Ritz procedure can be devised, and
this can be conveniently described in matrix form by
expressing the approximate eigenvector 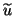 in matrix form with respect to
some basis and formulating the Petrov-Galerkin
conditions eq:4.21 for the basis of
in matrix form with respect to
some basis and formulating the Petrov-Galerkin
conditions eq:4.21 for the basis of  . This time we will need
two bases, one which we denote by
. This time we will need
two bases, one which we denote by 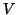 for the subspace
for the subspace 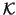 and the other,
denoted by
and the other,
denoted by 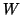 , for the subspace
, for the subspace  . We assume that these two bases are
biorthogonal, i.e., that
. We assume that these two bases are
biorthogonal, i.e., that
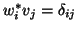 or
or
where 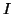 is the identity matrix.
Then, writing
is the identity matrix.
Then, writing 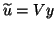 as before, the above Petrov-Galerkin condition
yields the same approximate problem as eq:4.18 except that the matrix
as before, the above Petrov-Galerkin condition
yields the same approximate problem as eq:4.18 except that the matrix
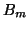 is now defined by
is now defined by
In order for a biorthogonal pair 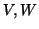 to exist, the following
additional assumption for
to exist, the following
additional assumption for  and
and 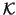 must hold.
must hold.
For any two bases 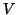 and
and 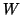 , of
, of 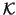 and
and  , respectively,
, respectively,
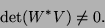 |
(13) |
Obviously this condition
does not depend on the particular bases selected and it is
equivalent to requiring that no vector of 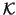 be orthogonal to
be orthogonal to  .
.
The approximate problem obtained for oblique projection methods has
the potential of being much worse conditioned than with orthogonal
projection methods. Therefore, one may wonder whether there is any
need for using oblique projection methods.
However, methods based on oblique projectors can offer
some advantages. In particular, they may be able to compute good
approximations to left as well as right eigenvectors
simultaneously. As will be seen later, there are also methods based on
oblique projection techniques which require far less storage than
similar orthogonal projections methods.
The disadvantages of working with the nonorthogonal 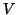 and
and 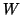 can be
reduced by combining this technique with a few steps of a (more
expensive) orthogonal projection method.
can be
reduced by combining this technique with a few steps of a (more
expensive) orthogonal projection method.





Next: Harmonic Ritz Values.
Up: Basic Ideas Y. Saad
Previous: Orthogonal Projection Methods.
Contents
Index
Susan Blackford
2000-11-20
![]() and
and ![]() , of
, of ![]() and
and ![]() , respectively,
, respectively,
![]() be orthogonal to
be orthogonal to ![]() .
.
![]() and
and ![]() can be
reduced by combining this technique with a few steps of a (more
expensive) orthogonal projection method.
can be
reduced by combining this technique with a few steps of a (more
expensive) orthogonal projection method.