




Next: Oblique Projection Methods.
Up: Basic Ideas Y. Saad
Previous: Basic Ideas Y. Saad
Contents
Index
Orthogonal Projection Methods.
Let  be an
be an 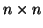 complex matrix and
complex matrix and 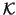 be an
be an
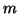 -dimensional subspace of
-dimensional subspace of 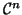 and consider the eigenvalue
problem of finding
and consider the eigenvalue
problem of finding
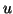 belonging to
belonging to 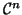 and
and 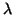 belonging to
belonging to
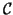 such that
such that
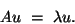 |
(7) |
An orthogonal projection technique onto the subspace 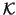 seeks an
approximate eigenpair
seeks an
approximate eigenpair
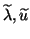 to the above
problem, with
to the above
problem, with 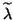 in
in 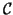 and
and 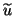 in
in 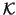 . This approximate
eigenpair is obtained by imposing the
following Galerkin condition:
. This approximate
eigenpair is obtained by imposing the
following Galerkin condition:
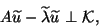 |
(8) |
or, equivalently,
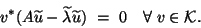 |
(9) |
In order to translate this into a matrix problem,
assume that an orthonormal basis
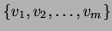 of
of 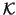 is available. Denote by
is available. Denote by 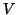 the matrix with column vectors
the matrix with column vectors
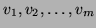 , i.e.,
, i.e.,
![$V = [v_1, v_2, \ldots , v_m] $](img682.png) .
Because we seek a
.
Because we seek a 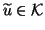 , it can be written as
, it can be written as
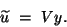 |
(10) |
Then, equation eq:4.16 becomes
Therefore, 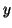 and
and
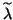 must satisfy
must satisfy
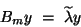 |
(11) |
with
B_m = V^ A V .
The approximate eigenvalues 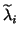 resulting from the projection process are
all the eigenvalues of the matrix
resulting from the projection process are
all the eigenvalues of the matrix 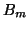 . The associated eigenvectors
are the vectors
. The associated eigenvectors
are the vectors 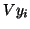 in which
in which 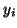 is an eigenvector of
is an eigenvector of 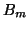 associated
with
associated
with 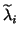 .
.
This procedure for numerically computing the Galerkin
approximations to the eigenvalues/eigenvectors of  is known as the
Rayleigh-Ritz procedure.
is known as the
Rayleigh-Ritz procedure.
RAYLEIGH-RITZ PROCEDURE
- Compute an orthonormal basis
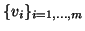 of the subspace
of the subspace 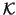 .
Let
.
Let
![$V = [v_1, v_2, \ldots , v_m] $](img682.png) .
.
- Compute
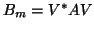 .
.
- Compute the eigenvalues of
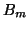 and select the
and select the 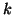 desired ones
desired ones
 , where
, where 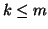 (for
instance the largest ones).
(for
instance the largest ones).
- Compute the eigenvectors
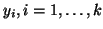 , of
, of 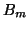 associated with
associated with
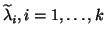 , and the
corresponding approximate eigenvectors of
, and the
corresponding approximate eigenvectors of  ,
,
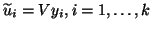 .
.
In implementations of this approach, one often does not compute the eigenpairs
of 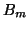 for each set of generated basis vectors.
The values
for each set of generated basis vectors.
The values 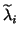 computed from this procedure are referred to as
Ritz values and the vectors
computed from this procedure are referred to as
Ritz values and the vectors 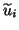 are the associated
Ritz vectors.
The numerical solution of the
are the associated
Ritz vectors.
The numerical solution of the 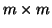 eigenvalue problem in steps 3
and 4 can be treated by standard library subroutines such as those in
LAPACK [12].
Another important note is that in step 4 one can replace
eigenvectors by Schur vectors to get approximate Schur vectors
eigenvalue problem in steps 3
and 4 can be treated by standard library subroutines such as those in
LAPACK [12].
Another important note is that in step 4 one can replace
eigenvectors by Schur vectors to get approximate Schur vectors 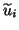 instead of approximate eigenvectors.
Schur vectors
instead of approximate eigenvectors.
Schur vectors 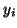 can be obtained in a numerically stable way and,
in general, eigenvectors are more sensitive to rounding errors
than are Schur vectors.
can be obtained in a numerically stable way and,
in general, eigenvectors are more sensitive to rounding errors
than are Schur vectors.





Next: Oblique Projection Methods.
Up: Basic Ideas Y. Saad
Previous: Basic Ideas Y. Saad
Contents
Index
Susan Blackford
2000-11-20
![]() is known as the
Rayleigh-Ritz procedure.
is known as the
Rayleigh-Ritz procedure.
![]() for each set of generated basis vectors.
The values
for each set of generated basis vectors.
The values ![]() computed from this procedure are referred to as
Ritz values and the vectors
computed from this procedure are referred to as
Ritz values and the vectors ![]() are the associated
Ritz vectors.
The numerical solution of the
are the associated
Ritz vectors.
The numerical solution of the ![]() eigenvalue problem in steps 3
and 4 can be treated by standard library subroutines such as those in
LAPACK [12].
Another important note is that in step 4 one can replace
eigenvectors by Schur vectors to get approximate Schur vectors
eigenvalue problem in steps 3
and 4 can be treated by standard library subroutines such as those in
LAPACK [12].
Another important note is that in step 4 one can replace
eigenvectors by Schur vectors to get approximate Schur vectors ![]() instead of approximate eigenvectors.
Schur vectors
instead of approximate eigenvectors.
Schur vectors ![]() can be obtained in a numerically stable way and,
in general, eigenvectors are more sensitive to rounding errors
than are Schur vectors.
can be obtained in a numerically stable way and,
in general, eigenvectors are more sensitive to rounding errors
than are Schur vectors.