




Next: Numerical Methods for Solving
Up: Spectral Transformations for QEP
Previous: Shift-and-Invert QEP.
Contents
Index
QEP with Cayley Transform.
With the so-called Cayley transform,
where the parameters 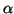 ,
, 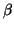 , and
, and 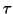 are chosen such that
are chosen such that
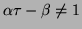 , the original QEP (9.1) becomes
, the original QEP (9.1) becomes
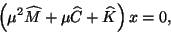 |
(262) |
where
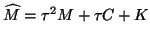 ,
,
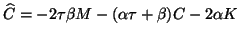 , and
, and
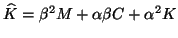 .
Eigenvalues
.
Eigenvalues 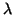 of the original QEP (9.1)
close to the antishift
of the original QEP (9.1)
close to the antishift 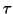 are
transformed into large (in modulus) eigenvalues
are
transformed into large (in modulus) eigenvalues 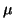 of the QEP
(9.18). Eigenvalues
of the QEP
(9.18). Eigenvalues 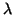 close to the shift
close to the shift
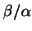 correspond to eigenvalues
correspond to eigenvalues 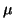 of (9.17) close to
of (9.17) close to 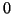 .
.
Note that the triple
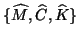 is symmetric
if that is the case for the real triple
is symmetric
if that is the case for the real triple 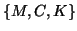 and if
and if 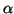 ,
, 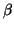 ,
and
,
and 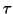 are real.
are real.
Susan Blackford
2000-11-20
![]() is symmetric
if that is the case for the real triple
is symmetric
if that is the case for the real triple ![]() and if
and if ![]() ,
, ![]() ,
and
,
and ![]() are real.
are real.