




Next: Golub-Kahan-Lanczos Bidiagonalization Procedure.
Up: Iterative Algorithms J.
Previous: Which Singular Values and
Contents
Index
Golub-Kahan-Lanczos Method
We have seen that the Hermitian eigenvalue problem and the singular
value decomposition are closely related. The singular values of
a matrix  are the square roots of the eigenvalues of
Hermitian matrix
are the square roots of the eigenvalues of
Hermitian matrix 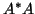 .
Consequently, we can calculate singular values by applying the
Hermitian Lanczos method to
.
Consequently, we can calculate singular values by applying the
Hermitian Lanczos method to 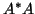 .
The matrix-vector product required by the algorithm
can be computed in the form
.
The matrix-vector product required by the algorithm
can be computed in the form
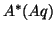 .
.
In this section we consider applying the Lanczos method
of §4.4 to 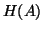 . The special
structure of
. The special
structure of 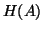 lets us choose a special starting vector
that leads to a cheaper algorithm that produces two sequences of
vectors, one intended to span the left singular vectors
and one for the right singular vectors.
In addition, it reduces
lets us choose a special starting vector
that leads to a cheaper algorithm that produces two sequences of
vectors, one intended to span the left singular vectors
and one for the right singular vectors.
In addition, it reduces  to bidiagonal form
to bidiagonal form  ;
i.e.,
;
i.e.,  is nonzero only on the main diagonal and first
superdiagonal. We derive it from first principles and then show
how it is related to Lanczos as described in §4.4.
is nonzero only on the main diagonal and first
superdiagonal. We derive it from first principles and then show
how it is related to Lanczos as described in §4.4.
Subsections





Next: Golub-Kahan-Lanczos Bidiagonalization Procedure.
Up: Iterative Algorithms J.
Previous: Which Singular Values and
Contents
Index
Susan Blackford
2000-11-20
![]() . The special
structure of
. The special
structure of ![]() lets us choose a special starting vector
that leads to a cheaper algorithm that produces two sequences of
vectors, one intended to span the left singular vectors
and one for the right singular vectors.
In addition, it reduces
lets us choose a special starting vector
that leads to a cheaper algorithm that produces two sequences of
vectors, one intended to span the left singular vectors
and one for the right singular vectors.
In addition, it reduces ![]() to bidiagonal form
to bidiagonal form ![]() ;
i.e.,
;
i.e., ![]() is nonzero only on the main diagonal and first
superdiagonal. We derive it from first principles and then show
how it is related to Lanczos as described in §4.4.
is nonzero only on the main diagonal and first
superdiagonal. We derive it from first principles and then show
how it is related to Lanczos as described in §4.4.