




Next: Residual Vector.
Up: Stability and Accuracy Assessments
Previous: Remarks on Clustered Eigenvalues.
Contents
Index
This is the general case for the definite matrix pair, and now
 may be singular. To be able to
handle infinite eigenvalues, it is standard practice [425] to
introduce a homogeneous representation
of an eigenvalue
may be singular. To be able to
handle infinite eigenvalues, it is standard practice [425] to
introduce a homogeneous representation
of an eigenvalue 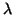 by a nonzero pair of numbers
by a nonzero pair of numbers
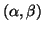 :
:
When 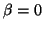 , such pairs represent eigenvalue
, such pairs represent eigenvalue 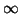 , and
this occurs when
, and
this occurs when  is singular.
Such representations are clearly not unique since
is singular.
Such representations are clearly not unique since
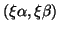 represents the same ratio for any
represents the same ratio for any 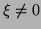 , and consequently the
same eigenvalue. So really a pair
, and consequently the
same eigenvalue. So really a pair
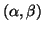 is a representative
from a class of pairs that give the same ratio.
The difference of two eigenvalues is measured by the
chordal metric:
for
is a representative
from a class of pairs that give the same ratio.
The difference of two eigenvalues is measured by the
chordal metric:
for
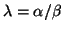 and
and
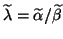 ,
,
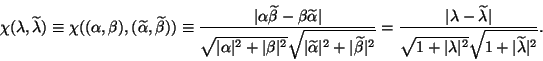 |
(99) |
An equivalent definition for a Hermitian matrix pair 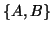 being a definite pair is that the Crawford number
being a definite pair is that the Crawford number
It can be proved [425] that if 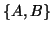 is a definite pair, then
is a definite pair, then
The decompositions (5.37) and (5.38)
give a complete picture of the underlying eigenvalue problems. In
fact, all eigenvalues are given by pairs
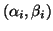 with
corresponding eigenvectors
with
corresponding eigenvectors 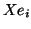 . If, in addition,
in (5.37) and (5.38)
. If, in addition,
in (5.37) and (5.38)
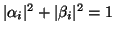 for all
for all 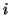 , then [423]
, then [423]
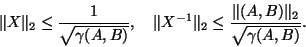 |
(103) |
Subsections





Next: Residual Vector.
Up: Stability and Accuracy Assessments
Previous: Remarks on Clustered Eigenvalues.
Contents
Index
Susan Blackford
2000-11-20
![]() with
corresponding eigenvectors
with
corresponding eigenvectors ![]() . If, in addition,
in (5.37) and (5.38)
. If, in addition,
in (5.37) and (5.38)
![]() for all
for all ![]() , then [423]
, then [423]