Remarks on Eigenvalue Computations to High Relative Accuracy.

Computation of eigenvalues to high accuracy has been attracting lots of attention over the last 10 years or so. Tremendous progress has been made in both theoretical understanding and numerical algorithms. But to give a detailed account is outside of the scope of this book. Interested readers are referred to the literature. On the algorithmic side there are the Demmel-Kahan QR method for bidiagonal singular value computations [123] and (two-sided) Jacobi methods for the eigenvalue problems of positive definite matrices. For the singular value computations [124,317,406], there are the bisection method for scaled diagonally dominant matrices [40], and for matrices with acyclic graphs [117,255], new implementations of the qd method [168,360] and Demmel's algorithms for structured matrices [115]. 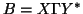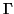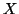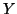More recently, [118] showed how to compute SVDs to high relative accuracy for matrices that can be factored accurately as $B=X\Gamma Y^*$, where $\Gamma$ is diagonal and $X$ and $Y$ are any well-conditioned matrices. 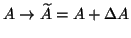On the theoretical side, analogous results to many celebrated theorems for absolute perturbations $A\to\wtd A=A+\Delta A$ are obtained for perturbations that are multiplicative, 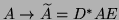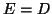$A\to\wtd A=D^*AE$ ($E=D$ when $A$ is Hermitian) [157,300,301,302,303,297].