




Next: Remarks on Eigenvalue Computations
Up: Stability and Accuracy Assessments
Previous: Error Bound for Computed
Contents
Index
In the case when the eigenvalue 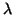 has one or more other eigenvalues of
has one or more other eigenvalues of  close by, in other words,
when
close by, in other words,
when 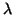 belongs to clustered eigenvalues,
as guaranteed by (4.54), the computed
belongs to clustered eigenvalues,
as guaranteed by (4.54), the computed 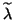 is still accurate as long as
is still accurate as long as 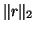 is tiny, but the computed
eigenvector
is tiny, but the computed
eigenvector 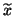 may be inaccurate because of the
appearance of the gap
may be inaccurate because of the
appearance of the gap 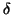 in the denominator of (4.56).
It turns out that each individual
eigenvector associated with the clustered eigenvalues
is very sensitive to perturbations,
but the eigenspace spanned by all the eigenvectors associated with
the clustered eigenvalues is not. Thus, for the clustered eigenvalues,
we should instead compute the entire eigenspace.
A theory along the lines given above can be established, starting with
a residual matrix
in the denominator of (4.56).
It turns out that each individual
eigenvector associated with the clustered eigenvalues
is very sensitive to perturbations,
but the eigenspace spanned by all the eigenvectors associated with
the clustered eigenvalues is not. Thus, for the clustered eigenvalues,
we should instead compute the entire eigenspace.
A theory along the lines given above can be established, starting with
a residual matrix
where 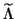 is diagonal with diagonal entries consisting of
approximations to all the eigenvalues in the cluster, and the columns of
is diagonal with diagonal entries consisting of
approximations to all the eigenvalues in the cluster, and the columns of
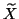 are the corresponding approximate eigenvectors.
Assume that
are the corresponding approximate eigenvectors.
Assume that 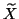 has orthonormal columns and that
has orthonormal columns and that 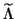 is
closer to
is
closer to 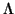 , the diagonal matrix whose diagonal entries
consist of all the eigenvalues in the cluster. Let
, the diagonal matrix whose diagonal entries
consist of all the eigenvalues in the cluster. Let 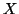 be the eigenvector
matrix associated with
be the eigenvector
matrix associated with 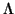 , and let
, and let 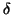 be the smallest difference
between any approximate eigenvalue in the diagonal of
be the smallest difference
between any approximate eigenvalue in the diagonal of 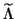 and those eigenvalues of
and those eigenvalues of  not presented in the diagonal of
not presented in the diagonal of 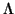 .
Then [101]
.
Then [101]
where
 is diagonal with diagonal entries being
the arccosines of the singular values of
is diagonal with diagonal entries being
the arccosines of the singular values of 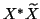 .
Because of the way it is defined, this gap is expected
to be big and thus
.
Because of the way it is defined, this gap is expected
to be big and thus
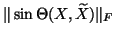 will be small as
long as
will be small as
long as 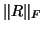 is.
is.





Next: Remarks on Eigenvalue Computations
Up: Stability and Accuracy Assessments
Previous: Error Bound for Computed
Contents
Index
Susan Blackford
2000-11-20