Proof

Let proc(I) be the processor that executes tile I. We have three cases to consider, depending upon whether proc(I) also executes both successors I' and I'', or exactly one of them, or none of them:

both successors:

proc(I)=proc(I')=proc(I'')
The same processor executes both successors. They are executed sequentially and the last one being executed cannot begin execution before time-step . As the result is proven.

one successor:

proc(I) = proc(I') and
(respectively proc(I) = proc(I'') and ). A communication is needed between I and I'' (respectively I and I'), hence (respectively )

no successor:

and
This case is similar to the previous one.

Back to the proof of the theorem, let the total execution time using P processors. Let Idle be the cumulated idle time of all processors during execution. Finally, let be the sequential execution time. Clearly,

Hence, to show that , we need to show that

The structure of the dependence graph does impose that some processors are idle at the beginning of the computation, which will lead to a lower bound for Idle. For instance, during the execution of tile (0,0), there are necessarily P-1 idle processors. To go on, we recursively define as follows (see Figure 5):

• , and
• for , is the one of the two successors of which is executed last: if , let I'=(i+1,j) and I''=(i,j+1) be the successors of tile I:
  • If , then , and we define S(k) as the remaining tiles in column j: ),
  • If , then , and we define S(k) as the remaining tiles in row i: ,

We know from Lemma 1 that for all ,

We prove by induction that for , at least P-k processors are kept idle between the beginning of the execution of and that of . This will lead to be result that

This will prove the desired result, because the same amount of idleness, so to speak, will be spent at the end of the computation (by symmetry of the dependence graph). Now, for the induction:

• Let k=1: is either (0,1) or (1,0). See Figure 5 where and . Between the the beginning of the execution of and that of , the only successors of that can be executed are in S(1). But all tasks in S(1) must be executed sequentially, hence between the beginning of the execution of and that of , at least (P-1) processors are kept idle.
• Assume that the hypothesis is true until step k. Between the beginning of the execution of and that of , at most one processor can be active in S(1), at most another one in S(2), , and at most one processor in S(k+1), so that at most k+1 processors can be active, or equivalently, at least P-(k+1) processors remain idle.

  
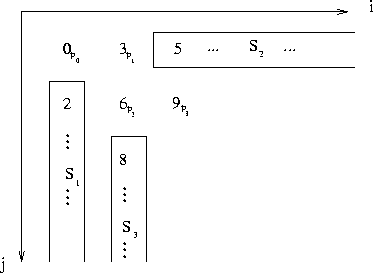
Figure 5: A schedule when and . Pivot tiles are labeled, and sets S(k) are framed.