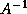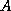In block factorizations a pivot block is generally forced to be sparse, typically of banded form, and that we need an approximation to its inverse that has a similar structure. Furthermore, this approximation should be easily computable, so we rule out the option of calculating the full inverse and taking a banded part of it.
The simplest approximation to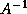 
is the diagonal matrix 
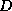of
the reciprocals of the diagonal of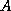 
: 
.
Figure: Algorithm for approximating the inverse of a banded matrix
Other possibilities were considered by
Axelsson and Eijkhout [15],
Axelsson and Polman [21],
Concus, Golub and Meurant [57],
Eijkhout and Vassilevski [90],
Kolotilina and Yeremin [141],
and Meurant [155]. One particular
example is given in figure 
. It has the attractive
theoretical property that, if the original matrix is symmetric
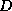positive definite and a factorization with positive diagonal can
be made, the approximation to the inverse is again symmetric positive
definite.
Banded approximations to the inverse of banded matrices have a
theoretical justification. In the context of partial differential
equations the diagonal blocks of the coefficient matrix are usually
strongly diagonally dominant. For such matrices, the elements of the
inverse have a size that is exponentially decreasing in their distance
from the main diagonal. See Demko, Moss and
Smith [65] for a general
proof, and Eijkhout and Polman [89] for a more detailed
analysis in the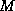 
-matrix case.