 (with
(with 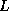 and
and 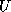 nonsingular triangular matrices),
solving a system proceeds in the usual way
(figure
nonsingular triangular matrices),
solving a system proceeds in the usual way
(figure
Incomplete factorizations can be given in various forms. If  (with
(with 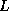 and
and 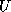 nonsingular triangular matrices),
solving a system proceeds in the usual way
(figure
nonsingular triangular matrices),
solving a system proceeds in the usual way
(figure ![]() ),
),
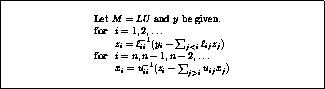
Figure: Preconditioner solve of a system 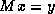 , with
, with 
but often incomplete factorizations are given as  (with
(with 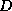 diagonal, and
diagonal, and
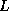 and
and 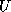 now strictly triangular matrices, determined through
the factorization process).
In that case, one could use either of the following equivalent
formulations for
now strictly triangular matrices, determined through
the factorization process).
In that case, one could use either of the following equivalent
formulations for 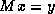 :
:
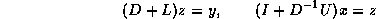
or
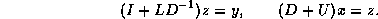
In either case, the diagonal elements are used twice (not three times
as the formula for 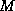 would lead one to expect), and since only
divisions with
would lead one to expect), and since only
divisions with 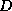 are performed, storing
are performed, storing 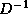 explicitly is the
practical thing to do.
explicitly is the
practical thing to do.
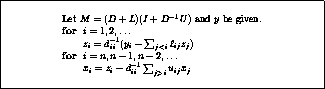
Figure: Preconditioner solve of a system 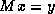 ,
with
,
with 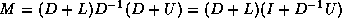 .
.
At the cost of some extra storage, one could store 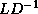 or
or 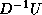 , thereby saving some computation.
Solving a system using the first formulation is
outlined in figure
, thereby saving some computation.
Solving a system using the first formulation is
outlined in figure ![]() . The second formulation is
slightly harder to implement.
. The second formulation is
slightly harder to implement.