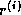 can be regarded as
the product
of
can be regarded as
the product
of  and an
and an 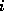 th degree polynomial in
th degree polynomial in 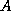 , that is
, that is
In BiCG, the residual vector 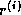 can be regarded as
the product
of
can be regarded as
the product
of  and an
and an 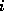 th degree polynomial in
th degree polynomial in 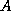 , that is
, that is
This same polynomial satisfies
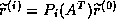 so that
so that
This suggests that if 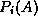 reduces
reduces  to a smaller
vector
to a smaller
vector 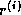 , then it might be advantageous to apply this
``contraction'' operator twice, and compute
, then it might be advantageous to apply this
``contraction'' operator twice, and compute 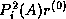 .
Equation (
.
Equation (![]() ) shows that the iteration coefficients can
still be recovered from these vectors, and it turns out to be easy to
find the corresponding approximations for
) shows that the iteration coefficients can
still be recovered from these vectors, and it turns out to be easy to
find the corresponding approximations for  . This
approach leads to the Conjugate Gradient Squared method (see
Sonneveld [192]).
. This
approach leads to the Conjugate Gradient Squared method (see
Sonneveld [192]).

Figure: The Preconditioned Conjugate Gradient Squared Method