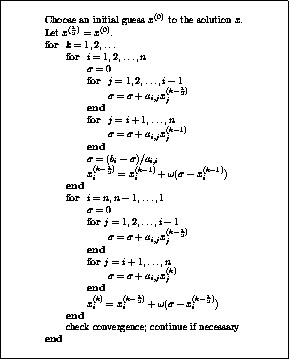The Symmetric Successive Overrelaxation Method





Next: Notes and References
Up: Stationary Iterative Methods
Previous: Choosing the Value
If we assume that the coefficient matrix 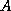 is symmetric, then the
Symmetric Successive Overrelaxation method, or SSOR, combines two SOR
sweeps together in such a way that the resulting iteration matrix is
similar to a symmetric matrix. Specifically, the
first SOR sweep is carried out as
in (
is symmetric, then the
Symmetric Successive Overrelaxation method, or SSOR, combines two SOR
sweeps together in such a way that the resulting iteration matrix is
similar to a symmetric matrix. Specifically, the
first SOR sweep is carried out as
in ( ), but in the second sweep the unknowns are
updated in the reverse order. That is, SSOR is a forward
SOR sweep followed by a
backward SOR sweep. The
similarity of the SSOR iteration matrix to a symmetric
matrix permits the application of SSOR as a preconditioner
for other iterative schemes for symmetric matrices. Indeed, this is
the primary motivation for SSOR since its convergence
rate , with an optimal value of
), but in the second sweep the unknowns are
updated in the reverse order. That is, SSOR is a forward
SOR sweep followed by a
backward SOR sweep. The
similarity of the SSOR iteration matrix to a symmetric
matrix permits the application of SSOR as a preconditioner
for other iterative schemes for symmetric matrices. Indeed, this is
the primary motivation for SSOR since its convergence
rate , with an optimal value of  , is
usually slower than the convergence rate of SOR with
optimal
, is
usually slower than the convergence rate of SOR with
optimal  (see Young [page 462]Yo:book). For details on
using SSOR as a preconditioner, see
Chapter
(see Young [page 462]Yo:book). For details on
using SSOR as a preconditioner, see
Chapter  .
.
In matrix terms, the SSOR iteration can be expressed as
follows:
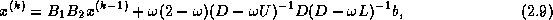
where
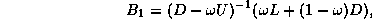
and
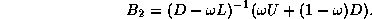
Note that 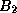 is simply the iteration matrix for SOR
from (
is simply the iteration matrix for SOR
from ( ), and that
), and that  is the same, but with the
roles of
is the same, but with the
roles of 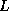 and
and 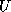 reversed.
reversed.
The pseudocode for the SSOR algorithm is given in
Figure  .
.
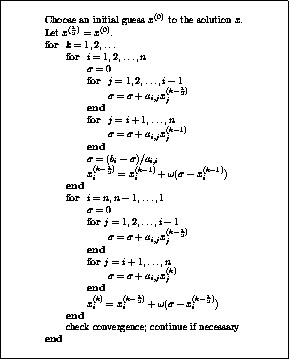
Figure: The SSOR Method
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
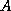 is symmetric, then the
Symmetric Successive Overrelaxation method, or SSOR, combines two SOR
sweeps together in such a way that the resulting iteration matrix is
similar to a symmetric matrix. Specifically, the
first SOR sweep is carried out as
in (
is symmetric, then the
Symmetric Successive Overrelaxation method, or SSOR, combines two SOR
sweeps together in such a way that the resulting iteration matrix is
similar to a symmetric matrix. Specifically, the
first SOR sweep is carried out as
in ( , is
usually slower than the convergence rate of SOR with
optimal
, is
usually slower than the convergence rate of SOR with
optimal  (see Young [page 462]Yo:book). For details on
using SSOR as a preconditioner, see
Chapter
(see Young [page 462]Yo:book). For details on
using SSOR as a preconditioner, see
Chapter 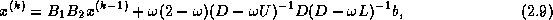
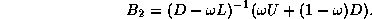
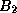 is simply the iteration matrix for SOR
from (
is simply the iteration matrix for SOR
from ( is the same, but with the
roles of
is the same, but with the
roles of 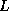 and
and 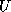 reversed.
reversed.