 equations in the linear system
equations in the linear system 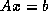 in isolation. If in
the
in isolation. If in
the 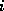 th equation
th equation
The Jacobi method is easily derived by examining each of
the  equations in the linear system
equations in the linear system 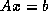 in isolation. If in
the
in isolation. If in
the 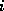 th equation
th equation

we solve for the value of  while assuming the other entries
of
while assuming the other entries
of  remain fixed, we obtain
remain fixed, we obtain
This suggests an iterative method defined by
which is the Jacobi method. Note that the order in which the equations are examined is irrelevant, since the Jacobi method treats them independently. For this reason, the Jacobi method is also known as the method of simultaneous displacements, since the updates could in principle be done simultaneously.
Simultaneous displacements, method of: Jacobi method.
In matrix terms, the definition of the Jacobi method
in (![]() ) can be expressed as
) can be expressed as
where the matrices 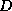 ,
, 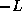 and
and 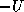 represent the diagonal, the
strictly lower-triangular, and the strictly upper-triangular parts of
represent the diagonal, the
strictly lower-triangular, and the strictly upper-triangular parts of 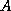 ,
respectively.
,
respectively.
The pseudocode for the Jacobi method is given in Figure ![]() .
Note that an auxiliary storage vector,
.
Note that an auxiliary storage vector,  is used in the
algorithm. It is not possible to update the vector
is used in the
algorithm. It is not possible to update the vector  in place,
since values from
in place,
since values from  are needed throughout the
computation of
are needed throughout the
computation of 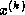 .
.