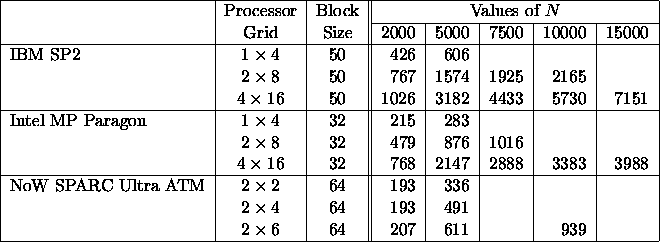
Table 5: Speed in Megaflop/s of PDGETRF for Square Matrices of Order N
The LU and Cholesky factorizations are the simplest block algorithms to derive for the block cyclic layout. Table 5 illustrates the speed of the ScaLAPACK routine for the LU factorization of a real matrix, PDGETRF. This corresponds to 64-bit floating-point arithmetic on all machines tested. The distribution block size is also used as the partitioning unit for the computation and communication phases. Table 6 gives similar results for the Cholesky factorization.

Table 5: Speed in Megaflop/s of PDGETRF for Square
Matrices of Order N
The right-looking variants of the LU and Cholesky factorizations were chosen for ScaLAPACK because they minimize the total communication volume, that is, the aggregated amount of data transferred between processors during the operation.
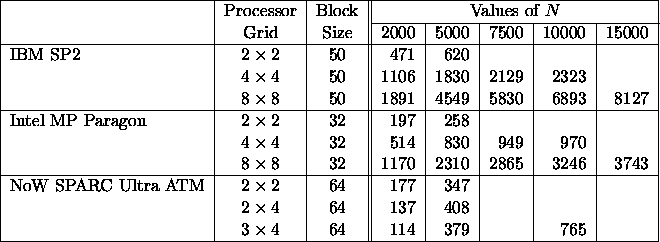
Table 6: Speed in Megaflop/s of PDPOTRF for Matrices of
Order N with UPLO=`U'
ScaLAPACK provides LU and Cholesky factorizations for band matrices. For small bandwidth, divide-and-conquer algorithms have been chosen despite their higher cost in terms of floating-point operations. A more detailed performance analysis can be found in [5].