An important performance
metric is parallel
efficiency. Parallel
efficiency, E(N, p),
for a problem of size
N on p processors
is defined in the usual
way [21, 28] by
where T(N,p) is the
runtime of the parallel
algorithm, and 
is the runtime of the
best sequential
algorithm. For
dense matrix
computations,
an implementation
is said to be
scalable if
the parallel
efficiency is
an increasing
function of
, the
problem size
per processor.
The algorithms
implemented in
the ScaLAPACK
library are
scalable in
this sense.
Figure 1 shows the scalability of the ScaLAPACK implementation of the LU factorization on the Intel XP/S MP Paragon. The figure shows the speed in Mflop/s of the ScaLAPACK LU factorization routine PDGETRF for different machine configurations. When the number of nodes is scaled by a constant factor (2 in the figure), the same efficiency or speed per node is achieved for equidistant problem sizes on a logarithmic scale. In other words, maintaining a constant memory use per node allows efficiency to be maintained. In practice, however, a slight degradation is acceptable. The ScaLAPACK driver routines in general feature the same scalability behavior up to a constant factor that depends on the exact number of floating-point operations and the total volume of data exchanged during the computation.
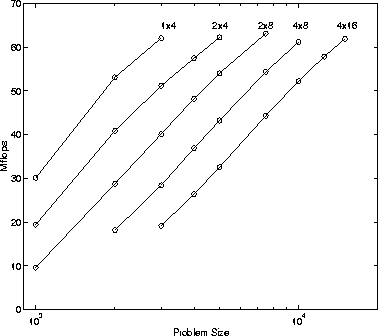
Figure 1: LU Performance per Intel Paragon node
The performance
of the algorithms
implemented in ScaLAPACK
is also measured in
megaflop/s per second
(or gigaflop/s
per second).
This measurement is appropriate
for large dense linear
algebra computations
since the computation
cost dominates the
communication cost.
In the following, the
time to execute one
floating-point operation
by one processor is
denoted 
. The
time to communicate
a message between
two processors is
approximated by a
linear function of
the number of items
communicated. The function is
the sum of the time
to prepare the message
for transmission (
)
and the time taken
by the message
to traverse the
network to its
destination, that is,
the product of its
length by the time
to transfer one
data item (
).
Alternatively,
is also called the
latency, since it
is the time to
communicate a
message of zero
length. On most
modern interconnection
networks, the order of
magnitude of the latency
varies between
a microsecond and
a millisecond.
The
bandwidth of the
network is also
referred to as
its throughput.
It is proportional
to the reciprocal
of . On modern
networks, the order
of magnitude of the
bandwidth is a
megabyte per
second.
For a scalable
algorithm with
held fixed,
one expects the
performance to
be proportional
to p. The
algorithms
implemented in
ScaLAPACK are
scalable in this
sense. It follows
that the execution
time of the ScaLAPACK
drivers can thus be
approximated by
The corresponding
parallel efficiency
can then be
approximated
by
Equation 1
illustrates, in
particular, that
the communication
versus computation
performance ratio
of a distributed-memory concurrent
computer significantly
affects parallel
efficiency. The
ratio of the latency
to the time per flop
greatly
affects the parallel
efficiency of small
problems. The ratio
of the network
throughput to
the flop rate
significantly
affects the
parallel
efficiency
of medium-sized
problems. For
large
problems, the
processor flop
rate 
is the dominant
factor contributing
to the parallel
efficiency of
the parallel
algorithms
implemented
in ScaLAPACK.