Restructuring Algorithms



Next: Summary
Up: Computation and Communication
Previous:
The LINPACK Benchmark
Advanced-architecture processors
are usually based on
memory hierarchies.
By
restructuring algorithms to exploit
this hierarchical organization, one can gain high performance.
A hierarchical memory structure involves a sequence of computer
memories ranging from a small, but very fast memory at
the bottom to a large, but slow memory at the top. Since a
particular memory in the hierarchy (call it  ) is not as big as the memory
at the next level (
) is not as big as the memory
at the next level (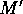 ), only part of the information in
), only part of the information in 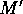 will be contained
in
will be contained
in  . If a reference is made to information that is in
. If a reference is made to information that is in  , then it is
retrieved as usual. However, if the information is not in
, then it is
retrieved as usual. However, if the information is not in  , then it must
be retrieved from
, then it must
be retrieved from 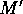 , with a loss of time. To avoid repeated
retrieval, information is transferred from
, with a loss of time. To avoid repeated
retrieval, information is transferred from 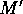 to
to  in blocks, the
supposition being that if a program references an item in a particular block, the
next reference is likely to be in the same block. Programs having this
property are said to have
locality of reference.
Typically, there is a certain startup time associated with getting
the first memory reference in a block.
This startup is amortized over the block move.
in blocks, the
supposition being that if a program references an item in a particular block, the
next reference is likely to be in the same block. Programs having this
property are said to have
locality of reference.
Typically, there is a certain startup time associated with getting
the first memory reference in a block.
This startup is amortized over the block move.
Processors such as the IBM RS/6000, DEC Alpha, Intel 860, etc
all have an additional
level of memory between the main memory and the registers of the
processor.
This memory, referred to as
cache.
To come close
to gaining peak performance, one
must optimize the use of this level of memory (i.e., retain information
as long as possible before the next access to main memory),
obtaining as much reuse as possible.
In the second benchmark, the problem size is larger
(matrix of order 1000), and
modifying or replacing the algorithm
and software is permitted to achieve as high an execution rate as possible.
The algorithm used for the 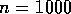 problem makes better use of
the memory hierarchy by utilizing the data in cache.
Thus, the hardware
had more opportunity for reaching near-asymptotic rates.
An important constraint, however, is that
all optimized programs maintain the
same relative accuracy as standard techniques,
such as Gaussian elimination
used in LINPACK.
problem makes better use of
the memory hierarchy by utilizing the data in cache.
Thus, the hardware
had more opportunity for reaching near-asymptotic rates.
An important constraint, however, is that
all optimized programs maintain the
same relative accuracy as standard techniques,
such as Gaussian elimination
used in LINPACK.
We have converted the floating point execution rates observed for each problem
to operations per cycle and also calculated the number of cycles
consumed, as overhead (latency), during communication.
For the LINPACK 100 test, many processors achieve one floating
point operation every four cycles, even though the process has the
ability to deliver much more than this.
The primary reason for this lack of performance relates
to the poor compiler generated code and the algorithm's
ineffective use of the memory hierarchy.
There are a few exceptions, most notably the IBM SP-2's processor.
The RS/6000-590 processor is able to achieve two floating point
operations per cycle for the LINPACK 100 test.
The compiler and the cache structure work together on
the RS/6000-590 and is able to achieve this rate.
There are also examples of poor performance on some of the
first generation parallel machines, such as the nCUBE 1 and 2
and the Intel iPSC/2. These processors are able to achieve only .01
to .04 floating point operations per cycle.
For the larger test case, LINPACK 1000, most of the processors achieve
70 to 80 % of their peak.



Next: Summary
Up: Computation and Communication
Previous:
The LINPACK Benchmark
Jack Dongarra
Fri Aug 4 04:24:58 EDT 1995
 ) is not as big as the memory
at the next level (
) is not as big as the memory
at the next level (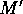 ), only part of the information in
), only part of the information in 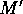 will be contained
in
will be contained
in  . If a reference is made to information that is in
. If a reference is made to information that is in  , then it is
retrieved as usual. However, if the information is not in
, then it is
retrieved as usual. However, if the information is not in  , then it must
be retrieved from
, then it must
be retrieved from 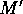 , with a loss of time. To avoid repeated
retrieval, information is transferred from
, with a loss of time. To avoid repeated
retrieval, information is transferred from 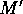 to
to  in blocks, the
supposition being that if a program references an item in a particular block, the
next reference is likely to be in the same block. Programs having this
property are said to have
locality of reference.
Typically, there is a certain startup time associated with getting
the first memory reference in a block.
This startup is amortized over the block move.
in blocks, the
supposition being that if a program references an item in a particular block, the
next reference is likely to be in the same block. Programs having this
property are said to have
locality of reference.
Typically, there is a certain startup time associated with getting
the first memory reference in a block.
This startup is amortized over the block move.
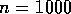 problem makes better use of
the memory hierarchy by utilizing the data in cache.
Thus, the hardware
had more opportunity for reaching near-asymptotic rates.
An important constraint, however, is that
all optimized programs maintain the
same relative accuracy as standard techniques,
such as Gaussian elimination
used in LINPACK.
problem makes better use of
the memory hierarchy by utilizing the data in cache.
Thus, the hardware
had more opportunity for reaching near-asymptotic rates.
An important constraint, however, is that
all optimized programs maintain the
same relative accuracy as standard techniques,
such as Gaussian elimination
used in LINPACK.