Non-self-adjoint Eigenproblems



Next: Problem Representation
Up: Desired Spectral Information
Previous: Self-adjoint Eigenproblems
An  -by-
-by- non-Hermitian matrix has
non-Hermitian matrix has  eigenvalues, which can be
anywhere in the complex plane. A non-self-adjoint regular pencil has
from 0 to
eigenvalues, which can be
anywhere in the complex plane. A non-self-adjoint regular pencil has
from 0 to  eigenvalues, which can be anywhere in the extended
complex plane. Thus some of the choices in the self-adjoint case do
not apply here. Instead, the following choices of spectral information
are possible:
eigenvalues, which can be anywhere in the extended
complex plane. Thus some of the choices in the self-adjoint case do
not apply here. Instead, the following choices of spectral information
are possible:
- All the eigenvalues.
- All the eigenvalues in some specified region of the complex plane,
such as
- The peripheral eigenvalues (when the spectrum is seen as a set
in the complex plane), such as the 10 rightmost eigenvalues.
- Eigenvalues in a given compact region, such as the unit disk.
- Eigenvalues in a given unbounded region, such as the
left half plane, or (a region around) the imaginary axis.
As before, the desired accuracy of the eigenvalues may be specified.
For each of these choices, the user can also compute the corresponding
(left or right) eigenvectors, or Schur vectors. Since the eigenvalues
of a non-Hermitian matrix can be very ill-conditioned, it is sometimes
hard to find all eigenvalues within a given region with certainty.
For eigenvalues that are clustered together, the user may choose to
estimate the mean of the cluster, or even the
 -pseudospectrum, the smallest region in the complex plane
which contains all the eigenvalues of all matrices
-pseudospectrum, the smallest region in the complex plane
which contains all the eigenvalues of all matrices 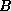 differing from
the given matrix
differing from
the given matrix  by at most
by at most  :
: 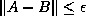 .
The user may also choose to compute the associated invariant
(or deflating or reducing) subspaces (left or right) instead of
individual eigenvectors. However, due to the potential ill-conditioning
of the eigenvalues, there is no guarantee that the invariant subspace
will be well-conditioned.
.
The user may also choose to compute the associated invariant
(or deflating or reducing) subspaces (left or right) instead of
individual eigenvectors. However, due to the potential ill-conditioning
of the eigenvalues, there is no guarantee that the invariant subspace
will be well-conditioned.
A singular pencil has a more complicated eigenstructure, as defined by
the Kronecker Canonical Form, a generalization of the Jordan Canonical Form
[41][23]. Instead of invariant or deflating subspaces,
we say a singular pencil has reducing subspaces.
Table 3 spells
out the possibilities. In addition to the notation used in the last section,
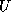 matrices denote generalized upper triangular (singular pencils only),
matrices denote generalized upper triangular (singular pencils only),
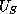 matrices are generalized upper triangular in staircase form
(singular pencils only),
matrices are generalized upper triangular in staircase form
(singular pencils only),
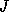 is in Jordan form, and
is in Jordan form, and 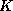 is in Kronecker form.
As before, these can be partial decompositions, when
is in Kronecker form.
As before, these can be partial decompositions, when 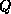 ,
, 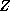 ,
,
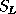 and
and 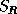 are
are  -by-
-by- instead of
instead of  -by-
-by- .
.

Table 3: The Possible ``Eigendecompositions'' of Non-self-adjoint
Eigenproblems
In addition to these decompositions, the user may request condition numbers for
any of the
computed quantities (eigenvalues, means of eigenvalue clusters, eigenvectors,
invariant/deflating/reducing subspaces). Given computed values for eigenvalues,
eigenvectors,
and/or subspaces, the user may also request an a posteriori error bound based
on a
computed residual.



Next: Problem Representation
Up: Desired Spectral Information
Previous: Self-adjoint Eigenproblems
Jack Dongarra
Wed Jun 21 02:35:11 EDT 1995
 -by-
-by- non-Hermitian matrix has
non-Hermitian matrix has  eigenvalues, which can be
anywhere in the complex plane. A non-self-adjoint regular pencil has
from 0 to
eigenvalues, which can be
anywhere in the complex plane. A non-self-adjoint regular pencil has
from 0 to  eigenvalues, which can be anywhere in the extended
complex plane. Thus some of the choices in the self-adjoint case do
not apply here. Instead, the following choices of spectral information
are possible:
eigenvalues, which can be anywhere in the extended
complex plane. Thus some of the choices in the self-adjoint case do
not apply here. Instead, the following choices of spectral information
are possible:
 -pseudospectrum, the smallest region in the complex plane
which contains all the eigenvalues of all matrices
-pseudospectrum, the smallest region in the complex plane
which contains all the eigenvalues of all matrices 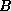 differing from
the given matrix
differing from
the given matrix  by at most
by at most 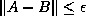 .
The user may also choose to compute the associated invariant
(or deflating or reducing) subspaces (left or right) instead of
individual eigenvectors. However, due to the potential ill-conditioning
of the eigenvalues, there is no guarantee that the invariant subspace
will be well-conditioned.
.
The user may also choose to compute the associated invariant
(or deflating or reducing) subspaces (left or right) instead of
individual eigenvectors. However, due to the potential ill-conditioning
of the eigenvalues, there is no guarantee that the invariant subspace
will be well-conditioned.
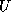 matrices denote generalized upper triangular (singular pencils only),
matrices denote generalized upper triangular (singular pencils only),
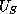 matrices are generalized upper triangular in staircase form
(singular pencils only),
matrices are generalized upper triangular in staircase form
(singular pencils only),
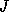 is in Jordan form, and
is in Jordan form, and 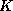 is in Kronecker form.
As before, these can be partial decompositions, when
is in Kronecker form.
As before, these can be partial decompositions, when 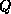 ,
, 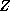 ,
,
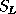 and
and 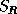 are
are  instead of
instead of 