




Next: 4.5.3 Comparison to Lattice
Up: 4.5 An Automata Model
Previous: 4.5.1 Introduction
The purpose of the lattice grain model is to predict the behavior of
large numbers of grains (10,000 to 1,000,000) on scales much larger
than a grain diameter. In this respect, it goes beyond the particle
dynamics calculations of Section 9.2, which are limited to no
more than 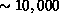 grains by currently available computing
resources [Cundall:79a], [Haff:87a;87b],
[Walton:84a], [Werner:87a]. The particle
dynamics models follow the motion of each individual grain exactly, and
may be formulated in one of two ways depending upon the model adopted
for particle-particle interactions.
grains by currently available computing
resources [Cundall:79a], [Haff:87a;87b],
[Walton:84a], [Werner:87a]. The particle
dynamics models follow the motion of each individual grain exactly, and
may be formulated in one of two ways depending upon the model adopted
for particle-particle interactions.
In one formulation, the interparticle contact times are assumed to be of
finite duration, and each particle may be in simultaneous contact with
several others [Cundall:79a], [Haff:87a], [Walton:84a],
[Werner:87a]. Each particle obeys Newton's law, F = ma, and a
detailed integration of the equations of motion of each particle is performed.
In this form, while useful for applications involving a much smaller number
of particles than LGrM allows, PDM cannot compete with LGrM for systems
involving large numbers of grains because of the complexity of PDM
``automata.''
In the second, simpler formulation, the interparticle contact times are
assumed to be of infinitesimal duration, and particles undergo only binary
collisions (the hard-sphere collisional models) [Haff:87b]. Hard-sphere
models usually rely upon a collision-list ordering of collision events to
avoid the necessity of checking all pairs of particles for overlaps at each
time step. In regions of high particle number density, collisions are very
frequent; and thus in problems where such high-density zones appear,
hard-sphere models spend most of their time moving particles through very
small distances using very small time steps. In granular flow, zones of
stagnation where particles are very nearly in contact much of the time, are
common, and the hard-sphere model is therefore unsuitable, at least in its
simplest form, as a model of these systems. LGrM avoids these difficulties
because its time-stepping is controlled, not by a collision list but by a scan
frequency, which in turn is a function of the speed of the fastest particle
and is independent of number density. Furthermore, although fundamentally a
collisional model, LGrM can also mimic the behavior of consolidated or
stagnated zones of granular material in a manner which will be described.





Next: 4.5.3 Comparison to Lattice
Up: 4.5 An Automata Model
Previous: 4.5.1 Introduction
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
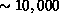 grains by currently available computing
resources [Cundall:79a], [Haff:87a;87b],
[Walton:84a], [Werner:87a]. The particle
dynamics models follow the motion of each individual grain exactly, and
may be formulated in one of two ways depending upon the model adopted
for particle-particle interactions.
grains by currently available computing
resources [Cundall:79a], [Haff:87a;87b],
[Walton:84a], [Werner:87a]. The particle
dynamics models follow the motion of each individual grain exactly, and
may be formulated in one of two ways depending upon the model adopted
for particle-particle interactions.




