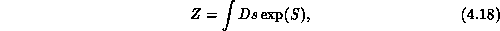
Spin models are simple statistical models of real systems, such as magnets, which exhibit the same behavior and hence provide an understanding of the physical mechanisms involved. Despite their apparent simplicity, most of these models are not exactly soluble by present theoretical methods. Hence, computer simulation is used. Usually, one is interested in the behavior of the system at a phase transition; the computer simulation reveals where the phase boundaries are, what the phases on either side are, and how the properties of the system change across the phase transition. There are two varieties of spins: discrete or continuous valued. In both cases, the spin variables are put on the sites of the lattice and only interact with their nearest neighbors. The partition function for a spin model is
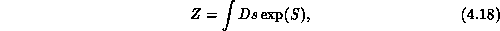
with the action being of the form
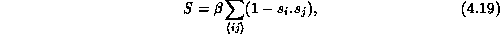
where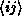 
denotes nearest neighbors, 
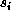is the spin
at site i, and 
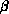is a coupling parameter which is proportional
to the interaction strength and inversely proportional to the
temperature. A great deal of work has been done over the years in
finding good algorithms for computer simulations of spin models;
recently some new, much better, algorithms have been discovered. These
so-called cluster algorithms are described in detail in
Section 12.6. Here, we shall describe results obtained from
using them to perform large-scale Monte Carlo simulations of several
spin models-both discrete and continuous.