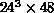Quantum chromodynamics (QCD) is the proposed theory of the so-called strong interactions that bind quarks and gluons together to form hadrons-the constituents of nuclear matter such as the proton and neutron. It also mediates the forces between hadrons and thus controls the formation of nuclei. The fundamental properties of QCD cannot be directly tested, but a wealth of indirect evidence supports this theory. The problem is that QCD is a nonlinear theory that is not analytically solvable. For the equivalent quantum field theories of weaker forces such as electromagnetism, approximations using perturbation expansions in the interaction strength give very accurate results. However, since the QCD interaction is so strong, perturbative approximations often fail. Consequently, few precise predictions can be made from the theory. This led to the introduction of a non-perturbative approximation based on discretizing four-dimensional space-time onto a lattice of points, giving a theory called lattice QCD, which can be simulated on a computer.
Most of the work on lattice QCD has been directed towards deriving the masses (and other properties) of the large number of hadrons, which have been found in experiments using high energy particle accelerators. This would provide hard evidence for QCD as the theory of the strong force. Other calculations have also been performed; in particular, the properties of QCD at finite (i.e., non-zero) temperature and/or density have been determined. These calculations model the conditions of matter in the early stages of the evolution of the universe, just after the Big Bang. Lattice calculations of other quantum field theories, such as the theory of the weak nuclear force, have also been performed. For example, numerical calculations have given estimates for the mass of the Higgs boson, which is currently the Holy Grail of experimental high energy physics, and one of the motivating factors for the construction of the, now cancelled, $10 billion Superconducting Supercollider.
One of the major problems in solving lattice QCD on a computer is that
the simulation of the quark interactions requires the computation of a
large, highly non-local matrix determinant, which is
extremely compute-intensive. We will discuss methods for calculating
this determinant later. For the moment, however, we note that, physically,
the determinant arises from the dynamics of the quarks. The simplest
way to proceed is thus to ignore the quark dynamics and work in the
so-called quenched approximation, with only gluonic degrees of
freedom. This should be a reasonable approximation, at least for heavy
quarks. However, even solving this approximate theory requires
enormous computing power. Current state-of-the-art quenched QCD
calculations are performed on lattices of size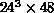 
, which
involves the numerical solution of a 21,233,664 dimensional integral.
The only way of solving such an integral is by Monte Carlo methods.