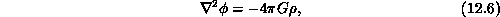
Two basic types of simulations exist for modelling systems of many particles: grid-based (point particles indirectly interacting with one another through the potential calculated from equivalent particle densities on a mesh) and particle-based (point particles directly interacting with one another through potentials at their positions calculated from the other particles in the system). Grid-based solvers traditionally model continuum problems, such as fluid and gas systems like the one described in Section 9.3, and mixed particle-continuum systems. Particle-based solvers find more use modeling discrete systems such as stars within galaxies, as discussed in Section 12.4, or other rarefied gases. Many different physical systems, including electromagnetic interactions, gravitational interactions, and fluid vortex interactions all are governed by Poisson's Equation:
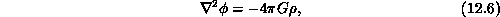
for the gravitational case. To evolve N particles in time, the exact solution to the problem requires calculating the force contribution to each particle from all other particles at each time step:
The 
operation count is prohibitive for simulations of more than a
few thousand particles commonly required to represent astrophysical and
vortex configurations of interest.
One method of decreasing the operation count utilizes grid-based
solvers which translate the particle problem into a continuum problem
by interpolating the particles onto a mesh representing density and
then solve the discretized equation. Initial implementations were
based upon fast fourier transform (FFT) and cloud-in-cell (CIC) methods which can calculate the potential of a
mass distribution on a three-dimensional grid with axes of length M
in 
operations, but at the cost of lower accuracy in
the force resolution. All of these algorithms are discussed
extensively by Hockney and Eastwood [Hockney:81a].
A newer type of grid-based solver for discretized equations classified as a multilevel or multigrid method has been in development for over a decade [Brandt:77a], [Briggs:87b]. Frequently, the algorithm utilizes a hierarchy of rectangular meshes on which a traditional relaxation scheme may be applied, but multiscale methods have expanded beyond any particular type of solver or even grids, per se. Relaxation methods effectively damp oscillatory error modes whose wave numbers are comparable to the grid size, but most of the iterations are spent propagating smooth, low-wave number corrections throughout the system. Multigrid utilizes this property by resampling the low-wave number residuals onto secondary, lower-resolution meshes, thereby shifting the error to higher wave numbers comparable to the grid spacing where relaxation is effective. The corrections computed on the lower-resolution meshes are interpolated back onto the original finer mesh and the combined solutions from the various mesh levels determine the result.
Many grid-based methods for particle problems have incorporated some
form of local direct-force calculation, such as the particle-particle/particle-mesh (PPPM) method or the method of
local corrections (MLC), to correct the force on a local subset of
particles. The grid is used to propagate the far-field component of
the force while direct-force calculations provide the near-field
component either completely or as a correction to the ``external''
potential. The computational cost strongly depends on the criterion
used to distinguish near-field objects from far-field objects.
Extremely inhomogeneous systems of densely clustered particles can
deteriorate to nearly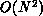 
if most of the particles are considered
neighbors requiring direct force computation.
A class of alternative techniques which have been implemented with great success utilize methods to efficiently calculate and combine the coefficients of an analytic approximation to the particle forces using spherical harmonic multipole expansions in three dimensions.
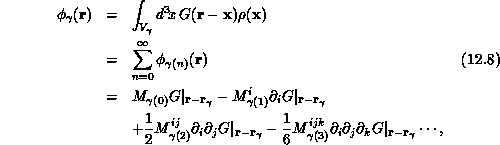
where the multipole moments
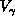are the disjoint spatial regions, and 
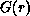is the Green's
function. Instead of integrating G over the volume 
, one may
compute the potential (and, in a similar manner, the gradient) at any
position by calculating the multipole moments which characterize the
density distribution in each region, evaluating G and its derivatives at
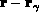, and summing over indices. This algorithm is
described more extensively in Section 12.4.
Not only does spatially sorting the particles into a
tree-type data structure provide an efficient database for individual
and collective particle information [Samet:90a], but the various
algorithms require and utilize the hierarchical grouping of particles
and combined information to calculate the force on each particle from
the multipole moments in 
operations or less.
Implementations for three-dimensional problems frequently use an oct-tree-a cube divided into eight octants of equal spatial volume which contain subcubes similarly divided. The cubes continue to nest until, depending on the algorithm, the cube contains either zero or one particles or a few particles of equal number to the other ``terminal'' cells. Binary trees which subdivide the volume with planes chosen to evenly divide the number of particles instead of the space also have been used [Appel:85a]; a single bifurcation separates two particles spaced arbitrarily close together while the oct-tree would require arbitrarily many subcubes refining one particular region. This approach may produce fewer artifacts by not imposing an arbitrary rectangular structure onto the simulation, but construction is more difficult and information about each cut must be stored and used throughout the computation.
Initial implementations for both grid-based and multipole techniques normally span the entire volume with a uniform resolution net in which to catch the result. While this is adequate for homogeneous problems, it either wastes computational effort and storage or sacrifices accuracy for problems which exhibit clustering and structure. Many of the algorithms described above provide enough flexibility to allow adaptive implementations which can conform to complicated particle distribution or accuracy constraints.