




Next: 12.6.2 Cluster Algorithms
Up: 12.6 Cluster Algorithms for
Previous: 12.6 Cluster Algorithms for
The goal of computer simulations of spin models is
to generate configurations of spins typical of statistical equilibrium
and measure physical observables on this ensemble of configurations.
The generation of configurations is traditionally performed by Monte
Carlo methods such as the
Metropolis algorithm [Metropolis:53a], which
produce configurations with a probability given by the Boltzmann
distribution 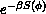 , where
, where 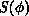 is the action, or
energy, of the system in configuration
is the action, or
energy, of the system in configuration 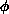 , and
, and 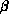 is the
inverse temperature. One of the main problems with these methods in
practice is that successive configurations are not statistically
independent, but rather are correlated with some autocorrelation time,
is the
inverse temperature. One of the main problems with these methods in
practice is that successive configurations are not statistically
independent, but rather are correlated with some autocorrelation time,
 , between effectively independent configurations.
, between effectively independent configurations.
A key feature of traditional (Metropolislike) Monte Carlo algorithms is
that the updates are local (i.e., one spin at a time is updated), and
its new value depends only on the values of spins which affect its
contribution to the action, that is, only on local (usually nearest
neighbor) spins. Thus, in a single step of the algorithm, information about
the state of a spin is transmitted only to its nearest neighbors. In order
for the system to reach a new effectively independent configuration, this
information must travel a distance of order the (static or spatial)
correlation length 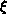 . As the information
executes a random walk around the lattice, one would suppose that the
autocorrelation time
. As the information
executes a random walk around the lattice, one would suppose that the
autocorrelation time 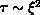 . However, in general,
. However, in general, 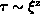 , where z is called the dynamical critical exponent.
Almost all numerical simulations of spin models have measured
, where z is called the dynamical critical exponent.
Almost all numerical simulations of spin models have measured 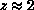 for local update algorithms. (See also Sections 4.3,
4.4, 7.3, 12.6, and 14.2).
for local update algorithms. (See also Sections 4.3,
4.4, 7.3, 12.6, and 14.2).
For a spin model with a phase transition, as
the inverse temperature 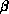 approaches the critical value,
approaches the critical value, 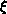 diverges to infinity so that the computational efficiency rapidly goes
to zero! This behavior is called critical slowing down (CSD),
and until very recently it has plagued Monte Carlo simulations of
statistical mechanical systems, in particular spin models, at or near
their phase transitions. Recently, however, several new ``cluster
algorithms'' have been introduced which decrease z dramatically by
performing nonlocal spin updates, thus reducing (or even
eliminating) CSD and facilitating much more efficient computer
simulations.
diverges to infinity so that the computational efficiency rapidly goes
to zero! This behavior is called critical slowing down (CSD),
and until very recently it has plagued Monte Carlo simulations of
statistical mechanical systems, in particular spin models, at or near
their phase transitions. Recently, however, several new ``cluster
algorithms'' have been introduced which decrease z dramatically by
performing nonlocal spin updates, thus reducing (or even
eliminating) CSD and facilitating much more efficient computer
simulations.





Next: 12.6.2 Cluster Algorithms
Up: 12.6 Cluster Algorithms for
Previous: 12.6 Cluster Algorithms for
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
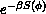 , where
, where 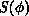 is the action, or
energy, of the system in configuration
is the action, or
energy, of the system in configuration 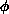 , and
, and 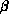 is the
inverse temperature. One of the main problems with these methods in
practice is that successive configurations are not statistically
independent, but rather are correlated with some autocorrelation time,
is the
inverse temperature. One of the main problems with these methods in
practice is that successive configurations are not statistically
independent, but rather are correlated with some autocorrelation time,
 , between effectively independent configurations.
, between effectively independent configurations.





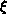 . As the information
executes a random walk around the lattice, one would suppose that the
autocorrelation time
. As the information
executes a random walk around the lattice, one would suppose that the
autocorrelation time 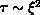 . However, in general,
. However, in general, 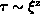 , where z is called the dynamical critical exponent.
Almost all numerical simulations of spin models have measured
, where z is called the dynamical critical exponent.
Almost all numerical simulations of spin models have measured 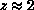 for local update algorithms. (See also Sections
for local update algorithms. (See also Sections 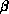 approaches the critical value,
approaches the critical value, 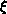 diverges to infinity so that the computational efficiency rapidly goes
to zero! This behavior is called critical slowing down (CSD),
and until very recently it has plagued Monte Carlo simulations of
statistical mechanical systems, in particular spin models, at or near
their phase transitions. Recently, however, several new ``cluster
algorithms'' have been introduced which decrease z dramatically by
performing nonlocal spin updates, thus reducing (or even
eliminating) CSD and facilitating much more efficient computer
simulations.
diverges to infinity so that the computational efficiency rapidly goes
to zero! This behavior is called critical slowing down (CSD),
and until very recently it has plagued Monte Carlo simulations of
statistical mechanical systems, in particular spin models, at or near
their phase transitions. Recently, however, several new ``cluster
algorithms'' have been introduced which decrease z dramatically by
performing nonlocal spin updates, thus reducing (or even
eliminating) CSD and facilitating much more efficient computer
simulations.