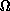Simple relaxation methods reduce the high-frequency components of the solution error by an order of magnitude in a few iterations. This observation is used to derive the multigrid method; see Brandt [Brandt:77a], Hackbusch [Hackbusch:85a]; Hackbusch and Trottenberg [Hackbusch:82a]. In the multigrid method, a smoothed problem is projected to a coarser grid. This coarse-grid problem is then solved recursively by smoothing and coarse-grid correction. The recursion terminates on the coarsest grid, where an exact solver is used. In the full multigrid method, a coarser grid is also used to compute an initial guess for the multigrid iteration on a finer grid. With this method, it is possible to solve the problem with an operation count proportional to the number of unknowns.
Multigrid methods are best understood for elliptic problems, that is,
the Poisson equation, stationary reaction-diffusion equations, implicit
time-steps in parabolic problems, and so on. However, the multigrid
approach is also successful for many other applications, from fluid
flow to computer vision. Parallelization issues are independent of
particular applications, and elliptic problems are a good test bed for
the study of concurrent multigrid. We chose two- and three-dimensional
stationary nonlinear reaction-diffusion equations in a rectangular
domain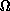 
as our model problem, that is,
with suitable boundary conditions.
To parallelize multigrid, we proceed as follows (see also [Velde:87a], [Velde:87b]). First, a sequential multigrid procedure is developed. Here, the basic numerical problems are addressed: which smoothing, restriction, and prolongation operators to use, the resolution required (size of the finest grid), the number of levels (size of the coarsest grid), and the coarsest-grid solver. Second, this sequential multigrid code is generalized to include local grid refinement (in the neighborhood of singularities, for example). Three basic problems are addressed in this second stage: the algorithmic aspect of local grid refinement, the numerical treatment of interior boundaries, and the relaxation of partially overlapping grid patches. In the third and last step, the multigrid code is parallelized. This can now be done without introducing new numerical issues. Each concurrent process starts a sequential multigrid procedure, each one locally refining to a particular subdomain. To achieve this, a communication operation for the exchange of interior boundary values is needed. Depending on the size of the coarsest grid, it might be required to develop, independently, a concurrent coarsest grid solver.
This parallelization strategy has the advantage that all numerical problems can be addressed in the sequential stages. Although our implementation is for regular grids, the same strategy is also valid for irregular grids.