




Next: 9.6.4 Concurrent Formulation
Up: 9.6.3 proto-Cdyn - Simulation
Previous: Template Structure
In general, the ``optimal'' ordering for the equations of a dynamic
simulation will in general be too difficult to establish , because
of the NP-hard issues involved in structure selection. However, many
important heuristics can be applied, such as those that precedence-order the
nonlinear equations, and those that permute the Jacobian structure to a more
nearly triangular or banded form [Duff:86a]. For the proto-Cdyn
simulator, we skirt these issues entirely, because it proves easy to arrange
a network of columns to produce a ``good structure''-a main block
tridiagonal Jacobian structure with off-block-diagonal structure for the
intercolumn connections, simply by taking the distillation columns with their
states in tray-by-tray, top-down (or bottom-up) order.
, because
of the NP-hard issues involved in structure selection. However, many
important heuristics can be applied, such as those that precedence-order the
nonlinear equations, and those that permute the Jacobian structure to a more
nearly triangular or banded form [Duff:86a]. For the proto-Cdyn
simulator, we skirt these issues entirely, because it proves easy to arrange
a network of columns to produce a ``good structure''-a main block
tridiagonal Jacobian structure with off-block-diagonal structure for the
intercolumn connections, simply by taking the distillation columns with their
states in tray-by-tray, top-down (or bottom-up) order.
Given a set of DAEs, and an ordering for the equations and states
(i.e., rows and columns of the Jacobian, respectively), we need to
partition these equations between the multicomputer nodes, according to a
two-dimensional process grid of shape 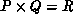 . The partitioning of
the equations forms, in main part, the so-called concurrent database.
This grid structure is illustrated in [Skjellum:90d, Figure 2.]. In
proto-Cdyn, we utilize a single process grid for the entire
Concurrent DASSL calculation. That is, we do not currently exploit the
Concurrent DASSL feature which allows explicit transformations
between the main calculational phases (see below). In each process column,
the entire set of equations is to be reproduced, so that any process column
can compute not only the entire residual vector for a prediction calculation,
but also, any column of the Jacobian matrix.
. The partitioning of
the equations forms, in main part, the so-called concurrent database.
This grid structure is illustrated in [Skjellum:90d, Figure 2.]. In
proto-Cdyn, we utilize a single process grid for the entire
Concurrent DASSL calculation. That is, we do not currently exploit the
Concurrent DASSL feature which allows explicit transformations
between the main calculational phases (see below). In each process column,
the entire set of equations is to be reproduced, so that any process column
can compute not only the entire residual vector for a prediction calculation,
but also, any column of the Jacobian matrix.
A mapping between the global and local equations must be created.
In the general case, it will be difficult to generate a closed-form
expression for either the global-to-local mapping or its inverse (that also
require 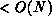 storage). At most, we will have on a hand a partial (or
weak) inverse in each process, so that the corresponding global index of each
local index will be available. Furthermore, in each node, a partial
global-to-local list of indices associated with the given node will be stored
in global sort order. Then, by binary search, a weak global-to-local mapping
will be possible in each process. That is, each process will be able to
identify if a global index resides within it, and the corresponding local
index. A strong mapping for row (column) indices will require communication
between all the processes in a process row (respectively, column). In the
foregoing, we make the tacit assumption that it is an unreasonable practice
to use storage proportional to the entire problem size N in each node,
except if this unscalability can be removed cheaply when necessary for large
problems.
storage). At most, we will have on a hand a partial (or
weak) inverse in each process, so that the corresponding global index of each
local index will be available. Furthermore, in each node, a partial
global-to-local list of indices associated with the given node will be stored
in global sort order. Then, by binary search, a weak global-to-local mapping
will be possible in each process. That is, each process will be able to
identify if a global index resides within it, and the corresponding local
index. A strong mapping for row (column) indices will require communication
between all the processes in a process row (respectively, column). In the
foregoing, we make the tacit assumption that it is an unreasonable practice
to use storage proportional to the entire problem size N in each node,
except if this unscalability can be removed cheaply when necessary for large
problems.
The proto-Cdyn simulator works with templates of specific
structure-each template is a form of a distillation tray and generates the
same number of integration states. It therefore skirts the need for weak
distributions. Consequently, the entire row-mapping procedure can be
accomplished using the closed-form general two-parameter distribution
function family 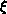 described in [Skjellum:90d], where the block size
B is chosen as the number of integration states per template. The
column-mapping procedure is accomplished with the one-parameter distribution
function family
described in [Skjellum:90d], where the block size
B is chosen as the number of integration states per template. The
column-mapping procedure is accomplished with the one-parameter distribution
function family 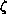 also described in [Skjellum:90d]. The effects of
row and column degree-of-scattering are described in [Skjellum:90d]
with attention to linear algebra performance.
also described in [Skjellum:90d]. The effects of
row and column degree-of-scattering are described in [Skjellum:90d]
with attention to linear algebra performance.





Next: 9.6.4 Concurrent Formulation
Up: 9.6.3 proto-Cdyn - Simulation
Previous: Template Structure
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
 , because
of the NP-hard issues involved in structure selection. However, many
important heuristics can be applied, such as those that precedence-order the
nonlinear equations, and those that permute the Jacobian structure to a more
nearly triangular or banded form [Duff:86a]. For the proto-Cdyn
simulator, we skirt these issues entirely, because it proves easy to arrange
a network of columns to produce a ``good structure''-a main block
tridiagonal Jacobian structure with off-block-diagonal structure for the
intercolumn connections, simply by taking the distillation columns with their
states in tray-by-tray, top-down (or bottom-up) order.
, because
of the NP-hard issues involved in structure selection. However, many
important heuristics can be applied, such as those that precedence-order the
nonlinear equations, and those that permute the Jacobian structure to a more
nearly triangular or banded form [Duff:86a]. For the proto-Cdyn
simulator, we skirt these issues entirely, because it proves easy to arrange
a network of columns to produce a ``good structure''-a main block
tridiagonal Jacobian structure with off-block-diagonal structure for the
intercolumn connections, simply by taking the distillation columns with their
states in tray-by-tray, top-down (or bottom-up) order.





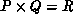 . The partitioning of
the equations forms, in main part, the so-called concurrent database.
This grid structure is illustrated in [
. The partitioning of
the equations forms, in main part, the so-called concurrent database.
This grid structure is illustrated in [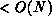 storage). At most, we will have on a hand a partial (or
weak) inverse in each process, so that the corresponding global index of each
local index will be available. Furthermore, in each node, a partial
global-to-local list of indices associated with the given node will be stored
in global sort order. Then, by binary search, a weak global-to-local mapping
will be possible in each process. That is, each process will be able to
identify if a global index resides within it, and the corresponding local
index. A strong mapping for row (column) indices will require communication
between all the processes in a process row (respectively, column). In the
foregoing, we make the tacit assumption that it is an unreasonable practice
to use storage proportional to the entire problem size N in each node,
except if this unscalability can be removed cheaply when necessary for large
problems.
storage). At most, we will have on a hand a partial (or
weak) inverse in each process, so that the corresponding global index of each
local index will be available. Furthermore, in each node, a partial
global-to-local list of indices associated with the given node will be stored
in global sort order. Then, by binary search, a weak global-to-local mapping
will be possible in each process. That is, each process will be able to
identify if a global index resides within it, and the corresponding local
index. A strong mapping for row (column) indices will require communication
between all the processes in a process row (respectively, column). In the
foregoing, we make the tacit assumption that it is an unreasonable practice
to use storage proportional to the entire problem size N in each node,
except if this unscalability can be removed cheaply when necessary for large
problems.
 described in [
described in [ also described in [
also described in [