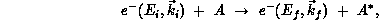





The collision of an electron with a molecule A may be illustrated schematically as
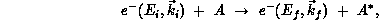
where 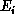 is the electron's initial kinetic energy and the momentum vector
is the electron's initial kinetic energy and the momentum vector
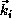 points in its initial direction of travel; after the collision,
the electron travels along
points in its initial direction of travel; after the collision,
the electron travels along 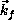 with kinetic energy
with kinetic energy 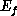 . If
. If  differs from
differs from 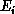 , the collision is said to be inelastic, and energy is
transferred to the target, leaving it in an excited state, denoted
, the collision is said to be inelastic, and energy is
transferred to the target, leaving it in an excited state, denoted 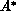 .
The quantity we seek is the probability of occurrence or cross section for
this process, as a function of the energies
.
The quantity we seek is the probability of occurrence or cross section for
this process, as a function of the energies 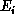 and
and 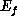 and of the angle
between the directions
and of the angle
between the directions 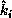 and
and 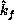 . (Since a gas is a very
large ensemble of randomly oriented molecules, orientational dependence of
these quantities for an asymmetric target A is averaged over in
calculations.)
. (Since a gas is a very
large ensemble of randomly oriented molecules, orientational dependence of
these quantities for an asymmetric target A is averaged over in
calculations.)
The SMC procedure [Lima:90a], [Takatsuka:81a;84a], a multichannel extension of Schwinger's variational principle [Schwinger:47a], is a method for obtaining cross sections for low-energy electron-molecule collision processes, including elastic scattering and vibrational or electronic excitation. As such, it is capable of accurately treating effects arising from electron indistinguishability and from polarization of the target by the charge of the incident electron, both of which can be important at low collision velocities. Moreover, it is formulated to be applicable to and efficient for molecules of arbitrary geometry.
The scattering amplitude  , a complex quantity whose
square modulus is proportional to the cross section, is approximated in the
SMC method as
, a complex quantity whose
square modulus is proportional to the cross section, is approximated in the
SMC method as
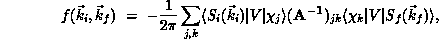
where 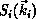 is an
is an 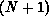 -electron interaction-free
wave function of the form
-electron interaction-free
wave function of the form
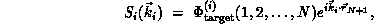
V is the interaction potential between the scattering electron and the
target, and the 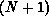 -electron functions
-electron functions 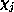 are spin-adapted Slater
determinants which form a linear variational basis set for approximating the
exact scattering wave functions
are spin-adapted Slater
determinants which form a linear variational basis set for approximating the
exact scattering wave functions 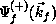 and
and
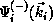 . The
. The 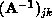 are elements of the
inverse of the matrix representation in the basis
are elements of the
inverse of the matrix representation in the basis 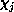 of the operator
of the operator
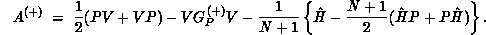
Here P is the projector onto open (energetically accessible) electronic states,
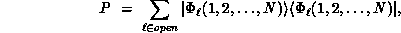
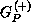 is the
is the 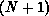 -electron Green's function projected onto open
channels, and
-electron Green's function projected onto open
channels, and 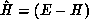 , where E is the total energy of the system and
H is the full Hamiltonian.
, where E is the total energy of the system and
H is the full Hamiltonian.
In our implementation, the 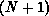 -electron functions
-electron functions 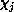 are
formed from antisymmetrized products of one-electron molecular
orbitals which are themselves combinations of
Cartesian Gaussian orbitals
are
formed from antisymmetrized products of one-electron molecular
orbitals which are themselves combinations of
Cartesian Gaussian orbitals
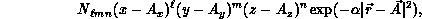
commonly used in molecular electronic-structure studies. Expansion of
the trial scattering wave function in such a basis of exponentially
decaying functions is possible since the trial function of the SMC
method need not satisfy scattering boundary conditions asymptotically
[Lima:90a],
[Takatsuka:81a;84a]. All matrix elements needed in the evaluation of
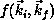 can then be obtained analytically, except those
of
can then be obtained analytically, except those
of 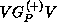 . These terms are evaluated numerically via a
momentum-space quadrature procedure [Lima:90a],
[Takatsuka:81a,84a].
Once all matrix elements are calculated, the final step in the
calculation is solution of a system of linear equations to obtain the
scattering amplitude
. These terms are evaluated numerically via a
momentum-space quadrature procedure [Lima:90a],
[Takatsuka:81a,84a].
Once all matrix elements are calculated, the final step in the
calculation is solution of a system of linear equations to obtain the
scattering amplitude 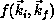 in the form given above.
in the form given above.
The computationally intensive step in the above formulation is the evaluation of large numbers of so-called ``primitive'' two-electron integrals
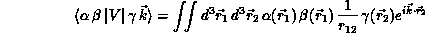
for all unique combinations of Cartesian Gaussians  ,
,
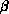 , and
, and 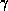 , and for a wide range of
, and for a wide range of 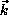 in both
magnitude and direction. These integrals are evaluated analytically by
a set of subroutines comprising approximately two thousand lines of
FORTRAN. Typical calculations might require
in both
magnitude and direction. These integrals are evaluated analytically by
a set of subroutines comprising approximately two thousand lines of
FORTRAN. Typical calculations might require 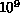 to
to 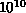 calls
to this integral-evaluation suite, consuming roughly 80% of the total
computation time. Once calculated, the primitive integrals are
assembled in appropriate combinations to yield the matrix elements
appearing in the variational expression for
calls
to this integral-evaluation suite, consuming roughly 80% of the total
computation time. Once calculated, the primitive integrals are
assembled in appropriate combinations to yield the matrix elements
appearing in the variational expression for 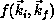 .
The original CRAY code performs this procedure in two steps: first, a
repeated linear transformation to integrals involving molecular
orbitals, then a transformation from the molecular-orbital integrals to
physical matrix elements. The latter step is equivalent to an
extremely sparse linear transformation, whose coefficients are
determined in an elaborate subroutine with a complicated logical flow.
.
The original CRAY code performs this procedure in two steps: first, a
repeated linear transformation to integrals involving molecular
orbitals, then a transformation from the molecular-orbital integrals to
physical matrix elements. The latter step is equivalent to an
extremely sparse linear transformation, whose coefficients are
determined in an elaborate subroutine with a complicated logical flow.




