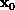Hipes has also compared the Gaussian-Jordan (GJ) and Gaussian Elimination (GE) algorithms for finding the inverse of a matrix [Hipes:88a]. This work was motivated by an application program that integrates a special system of ordinary differential equations that arise in chemical dynamics simulations [Hipes:87a], [Kuppermann:86a]. The sequential GJ and GE algorithms have the same operation count for matrix inversion. However, Hipes found the parallel GJ inversion has a more homogeneous load distribution, and requires fewer communication calls than GE inversion, and so should result in a more efficient parallel algorithm. Hipes has compared the two methods on the Caltech/JPL Mark II hypercube, and as expected found that GJ inversion algorithm to be the fastest.
Fox and Furmanski have also investigated matrix algorithms at Caltech
[Furmanski:88b]. Among the parallel algorithms they discuss is
the power method for finding the largest
eigenvalue, and corresponding
eigenvector, and a matrix A. This starts with an initial guess,
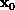, at the eigenvector, and then generates subsequent
estimates using
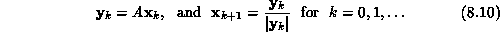
As k becomes large,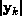 
tends to the eigenvalue with the largest
absolute value (except for a possible sign change), and 
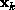tends to
the corresponding eigenvector. Since the main component of the algorithm is
matrix-vector multiplication, it can be done as discussed in
Section 8.1.2.
A more challenging algorithm to parallelize is the tridiagonalization of a symmetric matrix by Householder's method, which involves the application of a series of rotations to the original matrix. Although the basic operations involved in each rotation are straightforward (matrix-vector multiplication, scalar products, and so on), special care must be taken to balance the load. This is particularly difficult since the symmetry of the matrix A means that the basic structure being processed is triangular, and this is decomposed into a set of local triangular matrices in the individual processors. Load balance is optimized by scattering the rows over the processors, and the algorithm requires vectors to be broadcast and transposed.