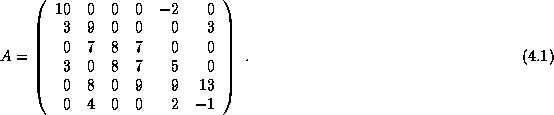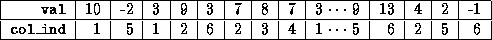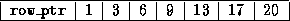Compressed Row Storage (CRS)





Next: Compressed Column Storage
Up: Survey of Sparse
Previous: Survey of Sparse
The Compressed Row and Column (in the next section) Storage formats
are the most general: they make absolutely no assumptions about the
sparsity structure of the matrix, and they don't store any unnecessary
elements. On the other hand, they are not very efficient, needing an
indirect addressing step for every single scalar operation in a matrix-vector
product or preconditioner solve.
The Compressed Row Storage (CRS) format puts the subsequent nonzeros of the
matrix rows in contiguous memory locations.
Assuming we have a nonsymmetric sparse matrix  , we create
, we create 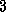 vectors:
one for floating-point numbers (val), and the other two for
integers (col_ind, row_ptr). The val vector
stores the values of the nonzero elements of the
matrix
vectors:
one for floating-point numbers (val), and the other two for
integers (col_ind, row_ptr). The val vector
stores the values of the nonzero elements of the
matrix  , as they are traversed in a row-wise fashion.
The col_ind vector stores
the column indexes of the elements in the val vector.
That is, if
, as they are traversed in a row-wise fashion.
The col_ind vector stores
the column indexes of the elements in the val vector.
That is, if  then
then 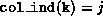 .
The row_ptr vector stores
the locations in the val vector that start a row, that is,
if
.
The row_ptr vector stores
the locations in the val vector that start a row, that is,
if  then
then 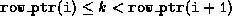 .
By convention, we define
.
By convention, we define 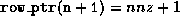 , where
, where  is
the number of nonzeros in the matrix
is
the number of nonzeros in the matrix  . The storage savings for this
approach is significant. Instead of storing
. The storage savings for this
approach is significant. Instead of storing 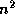 elements,
we need only
elements,
we need only  storage locations.
storage locations.
As an example, consider the nonsymmetric matrix  defined by
defined by
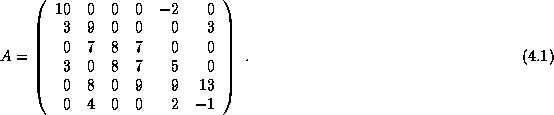
The CRS format for this matrix is then specified by the arrays
{val, col_ind, row_ptr} given below
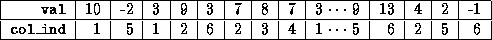
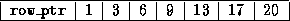
.
If the matrix  is symmetric, we need only store the upper (or
lower) triangular portion of the matrix. The trade-off is
a more complicated algorithm with a somewhat different pattern of data access.
is symmetric, we need only store the upper (or
lower) triangular portion of the matrix. The trade-off is
a more complicated algorithm with a somewhat different pattern of data access.
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
 , we create
, we create 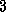 vectors:
one for floating-point numbers (val), and the other two for
integers (col_ind, row_ptr). The val vector
stores the values of the nonzero elements of the
matrix
vectors:
one for floating-point numbers (val), and the other two for
integers (col_ind, row_ptr). The val vector
stores the values of the nonzero elements of the
matrix  , as they are traversed in a row-wise fashion.
The col_ind vector stores
the column indexes of the elements in the val vector.
That is, if
, as they are traversed in a row-wise fashion.
The col_ind vector stores
the column indexes of the elements in the val vector.
That is, if  then
then 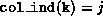 .
The row_ptr vector stores
the locations in the val vector that start a row, that is,
if
.
The row_ptr vector stores
the locations in the val vector that start a row, that is,
if  then
then 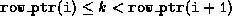 .
By convention, we define
.
By convention, we define 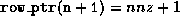 , where
, where  is
the number of nonzeros in the matrix
is
the number of nonzeros in the matrix  . The storage savings for this
approach is significant. Instead of storing
. The storage savings for this
approach is significant. Instead of storing 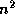 elements,
we need only
elements,
we need only  storage locations.
storage locations.