 is not positive definite, but symmetric, we can still
construct an orthogonal basis for the Krylov subspace
by three term recurrence relations.
Eliminating the
search directions
in equations (
is not positive definite, but symmetric, we can still
construct an orthogonal basis for the Krylov subspace
by three term recurrence relations.
Eliminating the
search directions
in equations (
When  is not positive definite, but symmetric, we can still
construct an orthogonal basis for the Krylov subspace
by three term recurrence relations.
Eliminating the
search directions
in equations (
is not positive definite, but symmetric, we can still
construct an orthogonal basis for the Krylov subspace
by three term recurrence relations.
Eliminating the
search directions
in equations (![]() )
and (
)
and (![]() ) gives a recurrence
) gives a recurrence
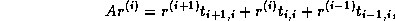
which can be written in matrix form as

where  is an
is an  tridiagonal matrix
tridiagonal matrix
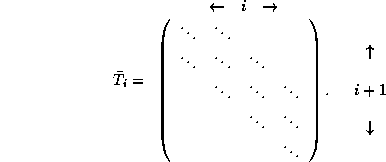
In this case we have the problem that 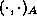 no
longer defines an inner product. However we can still try to minimize
the residual in the
no
longer defines an inner product. However we can still try to minimize
the residual in the 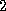 -norm by obtaining
-norm by obtaining

that minimizes

Now we exploit the fact that if  , then
, then
 is an orthonormal transformation with respect to
the current Krylov subspace:
is an orthonormal transformation with respect to
the current Krylov subspace:

and this final expression can simply be seen as a minimum norm least squares problem.
The element in the  position of
position of 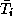 can be
annihilated by a simple Givens rotation and the resulting upper
bidiagonal system (the other subdiagonal elements having been removed
in previous iteration steps) can simply be solved, which leads to the
MINRES method (see Paige and Saunders [168]).
can be
annihilated by a simple Givens rotation and the resulting upper
bidiagonal system (the other subdiagonal elements having been removed
in previous iteration steps) can simply be solved, which leads to the
MINRES method (see Paige and Saunders [168]).
Another possibility is to solve the system
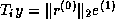 , as in the CG method (
, as in the CG method ( is the upper
is the upper
 part of
part of 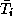 ). Other than in CG we cannot rely on
the existence of a Cholesky decomposition
(since
). Other than in CG we cannot rely on
the existence of a Cholesky decomposition
(since  is not positive
definite). An alternative is then to decompose
is not positive
definite). An alternative is then to decompose  by an
by an
 -decomposition. This again leads to simple recurrences and the
resulting method is known as SYMMLQ (see Paige and Saunders [168]).
-decomposition. This again leads to simple recurrences and the
resulting method is known as SYMMLQ (see Paige and Saunders [168]).