 such that the system
such that the system
Reduced system: Linear system obtained by eliminating certain variables from another linear system. Although the number of variables is smaller than for the original system, the matrix of a reduced system generally has more nonzero entries. If the original matrix was symmetric and positive definite, then the reduced system has a smaller condition number.
As we have seen earlier, a suitable preconditioner for CG is a
matrix  such that the system
such that the system

requires fewer iterations to solve than 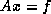 does, and for which
systems
does, and for which
systems 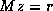 can be solved efficiently. The first property is
independent of the machine used, while the second is highly machine
dependent. Choosing the best preconditioner involves balancing those
two criteria in a way that minimizes the overall computation time.
One balancing approach used for matrices
can be solved efficiently. The first property is
independent of the machine used, while the second is highly machine
dependent. Choosing the best preconditioner involves balancing those
two criteria in a way that minimizes the overall computation time.
One balancing approach used for matrices  arising from
arising from 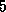 -point
finite difference discretization of second order elliptic partial
differential equations (PDEs) with Dirichlet boundary conditions
involves solving a reduced system. Specifically, for an
-point
finite difference discretization of second order elliptic partial
differential equations (PDEs) with Dirichlet boundary conditions
involves solving a reduced system. Specifically, for an  grid, we can use a point red-black ordering of the nodes to
get
grid, we can use a point red-black ordering of the nodes to
get
where  and
and 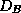 are diagonal, and
are diagonal, and 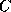 is a well-structured
sparse matrix with
is a well-structured
sparse matrix with 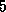 nonzero diagonals if
nonzero diagonals if  is even and
is even and
 nonzero diagonals if
nonzero diagonals if  is odd. Applying one step
of block Gaussian elimination (or computing the
Schur complement; see Golub and Van Loan [109]) we have
is odd. Applying one step
of block Gaussian elimination (or computing the
Schur complement; see Golub and Van Loan [109]) we have

which reduces to
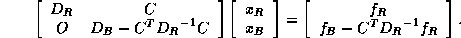
With proper scaling (left and right multiplication by  ),
we obtain from the second block equation the reduced system
),
we obtain from the second block equation the reduced system
where 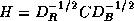 ,
, 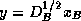 , and
, and 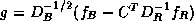 . The linear system (
. The linear system (![]() ) is of
order
) is of
order  for even
for even  and of order
and of order 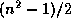 for odd
for odd  . Once
. Once
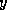 is determined, the solution
is determined, the solution  is easily retrieved from
is easily retrieved from 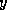 . The
values on the black points are those that would be obtained from a
red/black ordered SSOR preconditioner on the full system, so we expect
faster convergence.
. The
values on the black points are those that would be obtained from a
red/black ordered SSOR preconditioner on the full system, so we expect
faster convergence.
The number of nonzero coefficients is reduced, although the
coefficient matrix in (![]() ) has nine nonzero diagonals.
Therefore it has higher density and offers more data locality.
Meier and Sameh [150] demonstrate that the reduced system
approach on hierarchical memory
machines such as the Alliant FX/8 is over
) has nine nonzero diagonals.
Therefore it has higher density and offers more data locality.
Meier and Sameh [150] demonstrate that the reduced system
approach on hierarchical memory
machines such as the Alliant FX/8 is over
 times faster than unpreconditioned CG for Poisson's equation on
times faster than unpreconditioned CG for Poisson's equation on  grids with
grids with 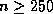 .
.
For  -dimensional elliptic PDEs, the reduced system approach yields
a block tridiagonal matrix
-dimensional elliptic PDEs, the reduced system approach yields
a block tridiagonal matrix 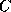 in (
in (![]() ) having diagonal
blocks of the structure of
) having diagonal
blocks of the structure of 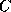 from the
from the 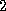 -dimensional case and
off-diagonal blocks that are diagonal matrices. Computing the reduced
system explicitly leads to an unreasonable increase in the
computational complexity of solving
-dimensional case and
off-diagonal blocks that are diagonal matrices. Computing the reduced
system explicitly leads to an unreasonable increase in the
computational complexity of solving 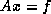 . The matrix products
required to solve (
. The matrix products
required to solve (![]() ) would therefore be performed implicitly
which could significantly decrease performance. However, as Meier and
Sameh show [150], the reduced system approach can still be about
) would therefore be performed implicitly
which could significantly decrease performance. However, as Meier and
Sameh show [150], the reduced system approach can still be about
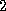 -
- times as fast as the conjugate gradient method with Jacobi
preconditioning for
times as fast as the conjugate gradient method with Jacobi
preconditioning for  -dimensional problems.
-dimensional problems.
Domain decomposition method: Solution method for
linear systems based on a partitioning of the physical domain
of the differential equation. Domain decomposition methods typically
involve (repeated) independent system solution on the subdomains,
and some way of combining data from the subdomains on the separator
part of the domain.