




Next: Arguments
Up: General Linear Systems
Previous: Purpose
Contents
Index
-
5.
- If
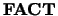 = 'E', then real row scaling factors
= 'E', then real row scaling factors
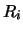 and/or real column scaling factors
and/or real column scaling factors 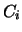 are computed to equilibrate
the system. The form of the equilibrated system depends on the
value of TRANS:
are computed to equilibrate
the system. The form of the equilibrated system depends on the
value of TRANS:
Depending on the value of EQUED determined during the equilibration,
the matrices 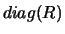 and/or
and/or
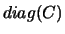 may be implicitly the identity matrix:
may be implicitly the identity matrix:
-
6.
- If FACT = 'N', the
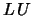 decomposition with row
interchanges is used to factor
decomposition with row
interchanges is used to factor  as
as 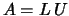 , where
, where 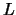 is a product
of permutation and unit lower triangular matrices with
is a product
of permutation and unit lower triangular matrices with 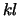 subdiagonals,
and
subdiagonals,
and 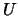 is upper triangular with
is upper triangular with 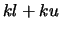 superdiagonals.
If
superdiagonals.
If 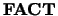 = 'E', the equilibrated matrix is factored as
= 'E', the equilibrated matrix is factored as 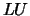 .
.
-
7.
- If some
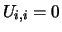 , so that
, so that 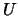 is singular, then the routine
returns with
is singular, then the routine
returns with
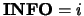 . Otherwise, an estimate of the condition
number of (the equilibrated)
. Otherwise, an estimate of the condition
number of (the equilibrated)  is found using the above factorization.
If the reciprocal of the condition number is less than machine precision,
is found using the above factorization.
If the reciprocal of the condition number is less than machine precision,
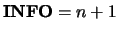 , where
, where 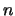 is the order of
is the order of  , is returned as a warning.
However, the routine still goes on
to solve for
, is returned as a warning.
However, the routine still goes on
to solve for 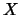 . Iterative refinement is
applied to improve the computed solution.
. Iterative refinement is
applied to improve the computed solution.
-
8.
- LA_GBSVX also optionally computes the reciprocal pivot
growth factor and, for each solution vector
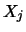 , the estimated
forward error bound and the componentwise relative backward error.
, the estimated
forward error bound and the componentwise relative backward error.





Next: Arguments
Up: General Linear Systems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
![\begin{displaymath}\begin{array}{c\vert c}
{\bf TRANS} & \mbox{ The equilibrate...
...g(C))^H]\;\,[diag(R)^{-1}X] =diag(C)\:B \\ \hline
\end{array} \end{displaymath}](img315.gif)

![\begin{displaymath}\begin{array}{c\vert c}
{\bf TRANS} & \mbox{ The equilibrate...
...g(C))^H]\;\,[diag(R)^{-1}X] =diag(C)\:B \\ \hline
\end{array} \end{displaymath}](img315.gif)
