




Next: Arguments
Up: General Linear Systems
Previous: Purpose
Contents
Index
-
1.
- If
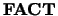 = 'E', then real row scaling factors
= 'E', then real row scaling factors
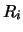 and/or real column scaling factors
and/or real column scaling factors 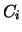 are computed to equilibrate
the system. The form of the equilibrated system depends on the
value of TRANS:
are computed to equilibrate
the system. The form of the equilibrated system depends on the
value of TRANS:
Depending on the value of EQUED determined during the equilibration,
the matrices
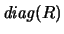 and/or
and/or
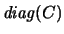 may be implicitly the identity matrix:
may be implicitly the identity matrix:
-
2.
- If
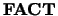 = 'N', matrix
= 'N', matrix  is factored as
is factored as 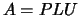 ,
where
,
where 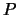 is a permutation matrix,
is a permutation matrix, 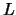 is unit lower triangular,
and
is unit lower triangular,
and 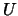 is upper triangular. If
is upper triangular. If 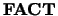 = 'E',
the equilibrated matrix is factored as
= 'E',
the equilibrated matrix is factored as  .
.
-
3.
- If some
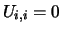 , so that
, so that 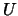 is singular, then the routine
returns with
is singular, then the routine
returns with
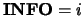 . Otherwise, an estimate of the condition
number of (the equilibrated)
. Otherwise, an estimate of the condition
number of (the equilibrated)  is found using the above factorization.
If the reciprocal of the condition number is less than machine precision,
is found using the above factorization.
If the reciprocal of the condition number is less than machine precision,
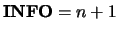 , where
, where 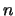 is the order of
is the order of  , is returned as a warning.
However, the routine still goes on
to solve for
, is returned as a warning.
However, the routine still goes on
to solve for 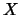 . Iterative refinement is
applied to improve the computed solution.
. Iterative refinement is
applied to improve the computed solution.
-
4.
- LA_GESVX also optionally computes the reciprocal pivot
growth factor and, for each solution vector
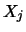 , the estimated
forward error bound and the componentwise relative backward error.
, the estimated
forward error bound and the componentwise relative backward error.





Next: Arguments
Up: General Linear Systems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
![\begin{displaymath}\begin{array}{c\vert c}
{\bf TRANS} & \mbox{ The equilibrate...
...hit{diag}(R)^{-1}X] =\mathit{diag}(C)\:B \\ \hline
\end{array}\end{displaymath}](img236.gif)

![\begin{displaymath}\begin{array}{c\vert c}
{\bf TRANS} & \mbox{ The equilibrate...
...hit{diag}(R)^{-1}X] =\mathit{diag}(C)\:B \\ \hline
\end{array}\end{displaymath}](img236.gif)
