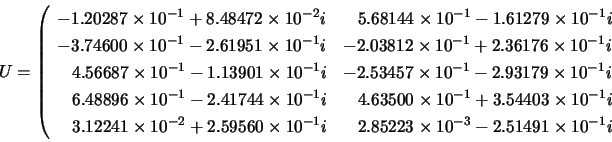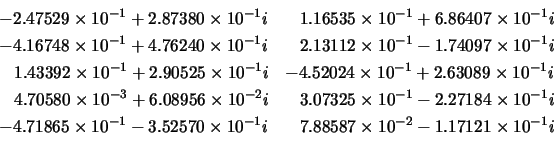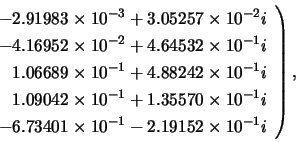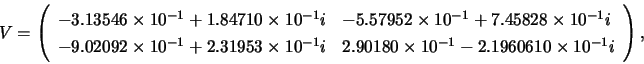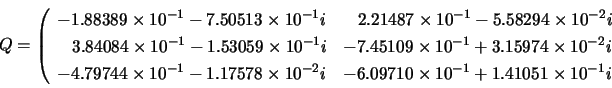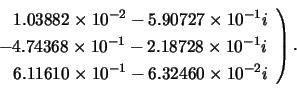Example 2 (from Program LA_GGSVD_EXAMPLE)

Arrays ${\bf A}$ and ${\bf B}$ on entry: As in Example 1.

The call:
CALL LA_GGSVD( A, B, ALPHA, BETA, K, L, U, V, Q, INFO=INFO )

A, ALPHA, BETA, K and L on exit: As in Example 1.
U, V, Q and INFO on exit:

$$\begin{array}{c} {\bf U} \\ \begin{array}{\vert ll} \hline... ...},-2.51491 \times 10^{-1}) \\ \hline \end{array} \end{array}$$

$$\begin{array}{c} {\bf U}\ continued \\ \begin{array}{ll} \... ...},-1.17121 \times 10^{-1}) \\ \hline \end{array} \end{array}$$

$$\begin{array}{l} {\bf U}\ continued \\ \begin{array}{r\ver... ...1},-2.19152 \times 10^{-1}) \\ \hline \end{array} \end{array}$$

$$\begin{array}{c} {\bf V} \\ \begin{array}{\vert ll\vert} \... ...-2.1960610 \times 10^{-1}) \\ \hline \end{array} \end{array}$$

$$\begin{array}{c} {\bf Q} \\ \begin{array}{\vert lll\vert} ... ...;\; 1.41051 \times 10^{-1}) \\ \hline \end{array} \end{array}$$

$$\begin{array}{c} {\bf Q}\ continued \\ \begin{array}{l\ver... ...y} \hspace{0.50 cm} \begin{array}{c} {\bf INFO} = 0 \end{array}$$

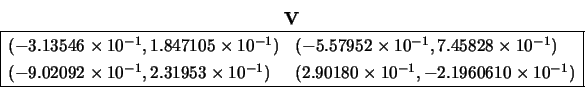
The generalized singular values of $(A,\,B)$ are as in Example 1.
Matrices $U$, $V$ and $Q$ are:

$$U=\left( \begin{array}{ll} -1.20287 \times 10^{-1} + 8.4847... ...\times 10^{-3} - 2.51491 \times 10^{-1}i \end{array} \right.$$

$$\left. \begin{array}{ll} -2.47529 \times 10^{-1} + 2.87380 ... ...\times 10^{-2} - 1.17121 \times 10^{-1}i \end{array} \right.$$

$$\left. \begin{array}{r} -2.91983 \times 10^{-3} + 3.05257 ... ...\times 10^{-1} - 2.19152 \times 10^{-1}i \end{array} \right),$$

$$V=\left( \begin{array}{ll} -3.13546 \times 10^{-1} + 1.8471... ...mes 10^{-1} - 2.1960610 \times 10^{-1}i \end{array} \right),$$

$$Q=\left( \begin{array}{ll} -1.88389 \times 10^{-1} - 7.505... ...es 10^{-1} + 1.41051 \times 10^{-1}i \\ \end{array} \right.$$

$$\left. \begin{array}{l} \;\;\; 1.03882 \times 10^{-2} - 5.9... ...s 10^{-1} - 6.32460 \times 10^{-2}i \\ \end{array} \right).$$