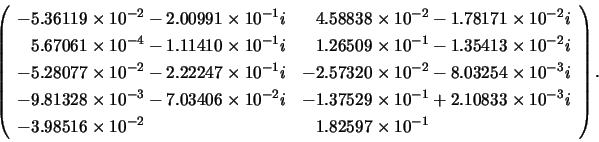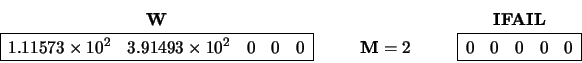
The call:
CALL LA_HPGVX( AP, BP, W, 2, Z= Z, IL=4, IU=5, M= M, &Note: wp is a work precision; wp ::= KIND(1.0)
IFAIL=IFAIL, ABSTOL=1.0E-3_wp )
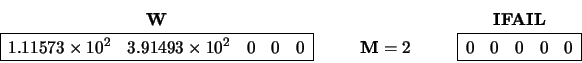

The last two eigenvalues of the problem
![]() are:
are:
The two eigenvectors converged successfully and are: