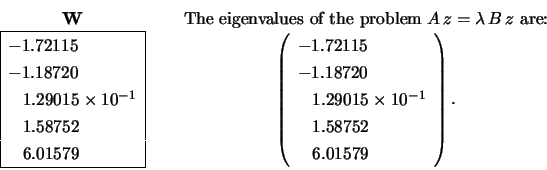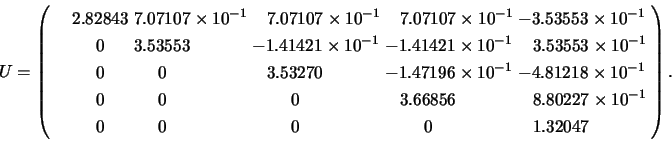Next: Example 2 (from Program
Up: Examples
Previous: Examples
Contents
Index
Arrays 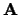 and
and 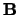 on entry:
on entry:
Elements marked * are not used by the routine.
The call:
CALL LA_SYGV( A, B, W )
B and 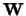 on exit:
on exit:
The triangular factor 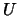 of the Cholesky factorization of
of the Cholesky factorization of 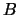 is:
is:
Susan Blackford
2001-08-19
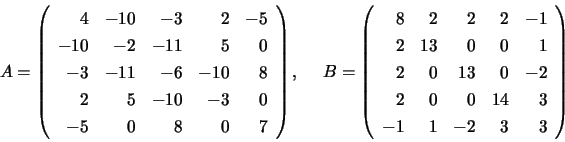
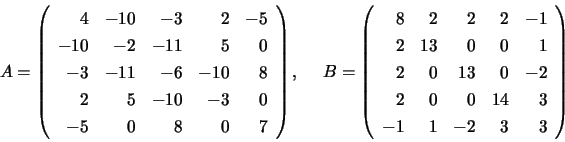

![]() on exit:
on exit: