The call:
CALL LA_GEEVX( A, WR, WI, 'B', ILO, IHI, SCALE, &
ABNRM, RCONDE, RCONDV )
![]() and RCONDV on exit:
and RCONDV on exit:
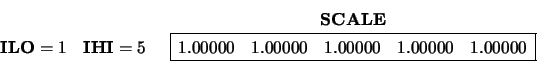
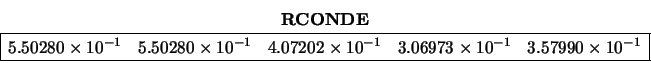

Matrix ![]() did not need balancing.
did not need balancing.
The ![]() norm of matrix
norm of matrix ![]() is 21.
is 21.
The reciprocal condition numbers of the eigenvalues are:
The reciprocal condition numbers of the right eigenvectors are: