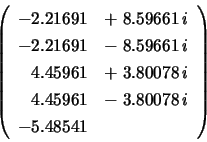Example (from Program LA_GEESX_EXAMPLE)

The results below are computed with $\epsilon = 1.19209 \times 10^{-7}$.
Matrix $A$ is the same as in Example 1 for LA_GEES.

Function SELECT is:

 		 LOGICAL FUNCTION SELECT( WR, WI ) 


USE LA_PRECISION, ONLY: WP $=>$ wp 


REAL(WP), INTENT(IN) :: WR, WI 


INTRINSIC EPSILON, ABS 


IF ( (ABS(WR) + ABS(WI) ) $<$ 20.0_WP ) THEN 


SELECT = .TRUE. 


ELSE 


SELECT = .FALSE. 


END IF 


END FUNCTION SELECT

The call:

 CALL LA_GEESX( A, WR, WI, SELECT=SELECT, SDIM=SDIM, & 


RCONDE=RCONDE, RCONDV=RCONDV )

WR, WI, SDIM, RCONDE and RCONDV on exit:

$$\begin{array}{cc} {\bf WR} \\ \begin{array}{\vert rrrrr\ve... ...4.45961 & 4.45961 & -5.48541 \\ \hline \end{array} \end{array}$$

$$\begin{array}{cc} {\bf WI} \\ \begin{array}{\vert rrrrr\ve... ...661 & 3.80078 & -3.80078 & 0 \\ \hline \end{array} \end{array}$$

$$\begin{array}{ccc} {\bf SDIM} = 5 & {\bf RCONDE} = 1.00000 & {\bf RCONDV} = 2.21900 \times 10^{1} \end{array}$$

The eigenvalues of matrix $A$ are:

$$\left( \begin{array}{rr} -2.21691 & +\; 8.59661\,i \\ -2.2... ...\ 4.45961 & -\; 3.80078\,i \\ -5.48541 \end{array} \right)$$

The reciprocal condition number for the average of the eigenvalues is 1.
The reciprocal condition number for the right invariant subspace is 2.21900$\times 10^{1}$.