Example (from Program LA_SYSVX_EXAMPLE)

The results below are computed with $\epsilon = 1.19209 \times 10^{-7}$.
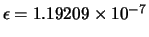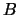Matrices $A$ and $B$ are the same as in Example 1 for LA_SYSV.

The call:
CALL LA_SYSVX( A, B, X, FERR= FERR, BERR= BERR, RCOND= RCOND )

FERR, BERR and RCOND on exit:

$$\begin{array}{c} {\bf FERR} \\ \begin{array}{\vert rrr\vert... ...5} & 1.42291 \times 10^{-5}\\ \hline \end{array} \end{array}$$

$$\begin{array}{c} {\bf BERR} \\ \begin{array}{\vert rrr\vert... ...8} & 2.48353 \times 10^{-9} \\ \hline \end{array} \end{array}$$

$$\begin{array}{c} {\bf RCOND} = 3.07451 \times 10^{-2} \end{array}$$

The forward and backward errors of the three solution vectors are:

$$\left( \begin{array}{ccc} 1.43778 \times 10^{-5} & 1.43778 \times 10^{-5} & 1.42291 \times 10^{-5} \end{array} \right),$$

$$\left( \begin{array}{ccc} 2.33236 \times 10^{-8} & 2.33236 \times 10^{-8} & 2.48353 \times 10^{-9} \end{array} \right).$$

The estimate of the reciprocal condition number of matrix $A$ is $3.07451 \times 10^{-2}$.

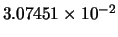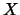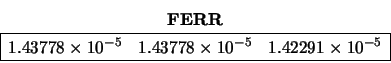
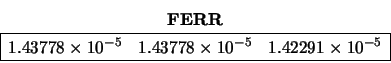
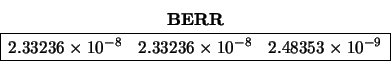
The computed solution $X$ is identical to that in Example 1 for LA_SYSV.