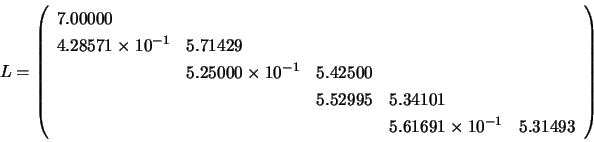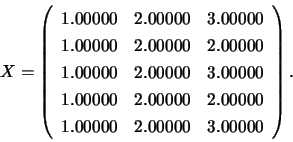Next: LA_PTSVX
Up: Arguments
Previous: Arguments
Contents
Index
The results below are computed with
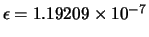 .
.
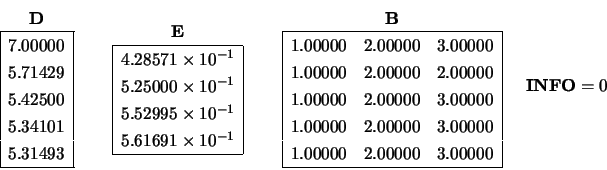
Arrays 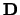 ,
, 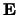 and
and 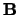 on entry:
on entry:
The call:
CALL LA_PTSV( D, E, B, INFO )
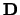 ,
, 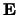 ,
, 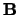 and
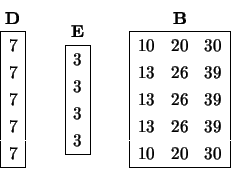
and  on exit:
on exit:
Matrices 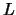 and
and 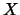 , where
, where 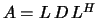 and
and 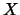 is the solution of the system
is the solution of the system
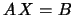 :
:
Susan Blackford
2001-08-19
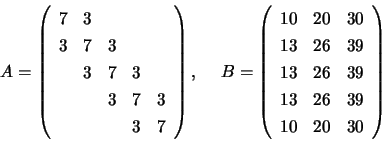
![]() ,
, ![]() ,
, ![]() and
and ![]() on exit:
on exit: