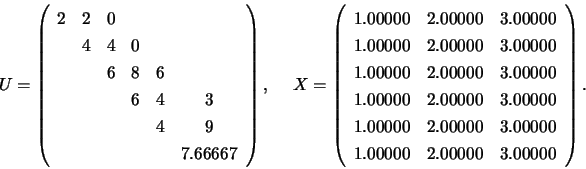Next: Symmetric/Hermitian Positive Definite Linear
Up: General Linear Systems
Previous: Arguments
Contents
Index
The results below are computed with
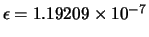 .
.
 is the same as in the example for LA_GTSV.
is the same as in the example for LA_GTSV.
The call:
CALL LA_GTSVX(DL, D, DU, B, X, DLF, DF, DUF, DU2, TRANS='T' )
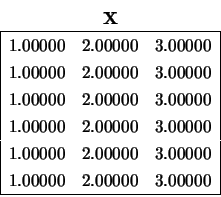
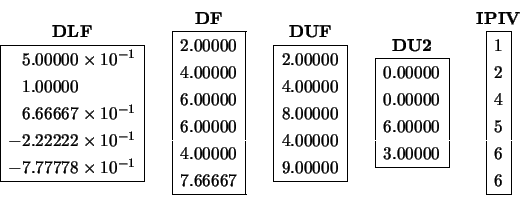
X, DLF, DF, DUF, DU2 and IPIV on exit:
Matrix 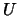 and the solution of the system
and the solution of the system  are:
are:
Susan Blackford
2001-08-19