This section contains performance numbers for selected LAPACK driver routines. These routines provide complete solutions for the most common problems of numerical linear algebra, and are the routines users are most likely to call:
We only present data on DGESDD for singular values only, and not DGESVD, because both use the same algorithm. We include both DGESVD and DGESDD for computing all the singular values and singular vectors to illustrate the speedup of the new algorithm DGESDD over its predecessor DGESVD: For 1000-by-1000 matrices DGESDD is between 6 and 7 times faster than DGESVD on most machines.
The above drivers are timed on a variety of computers. In addition, we present data on fewer machines to compare the performance of the five different routines for solving linear least squares problems, and several different routines for the symmetric eigenvalue problem. Again, the purpose is to illustrate the performance improvements in LAPACK 3.0.
Data is provided for PCs, shared memory parallel computers, and high performance workstations. All timings were obtained by using the machine-specific optimized BLAS available on each machine. For machines running the Linux operating system, the ATLAS[102] BLAS were used. In all cases the data consisted of 64-bit floating point numbers (double precision). For each machine and each driver, a small problem (N=100 with LDA=101) and a large problem (N=1000 with LDA=1001) were run. Block sizes NB = 1, 16, 32 and 64 were tried, with data only for the fastest run reported in the tables below. For DGEEV, ILO=1 and IHI=N. The test matrices were generated with randomly distributed entries. All run times are reported in seconds, and block size is denoted by nb. The value of nb was chosen to make N=1000 optimal. It is not necessarily the best choice for N=100. See Section 6.2 for details.
The performance data is reported using three or four statistics. First, the run-time in seconds is given. The second statistic measures how well our performance compares to the speed of the BLAS, specifically DGEMM. This ``equivalent matrix multiplies'' statistic is calculated as
We also include several figures comparing the speed of several routines for the symmetric eigenvalue problem and several least squares drivers to highlight the performance improvements in LAPACK 3.0.
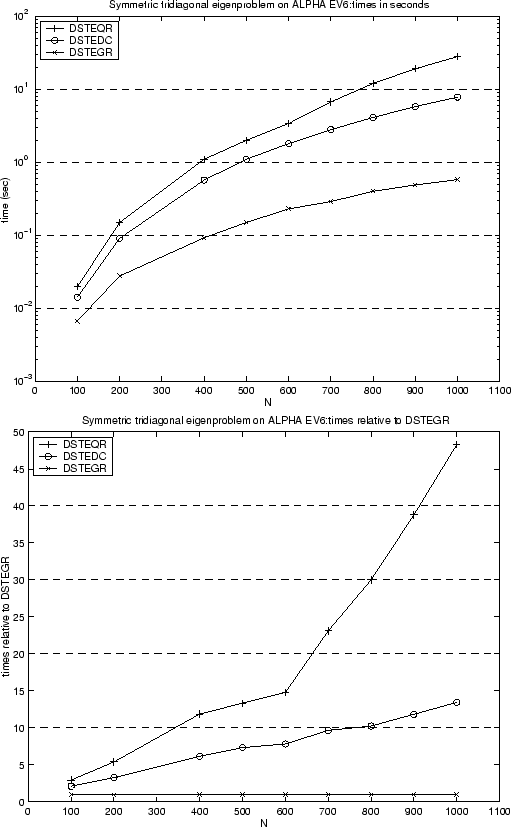
First consider Figure 3.1, which compares the performance of three routines, DSTEQR, DSTEDC and DSTEGR, for computing all the eigenvalues and eigenvectors of a symmetric tridiagonal matrix. The times are shown on a Compaq AlphaServer DS-20 for matrix dimensions from 100 to 1000. The symmetric tridiagonal matrix was obtained by taking a random dense symmetric matrix and reducing it to tridiagonal form (the performance can vary depending on the distribution of the eigenvalues of the matrix, but the data shown here is typical). DSTEQR (used in driver DSYEV) was the only algorithm available in LAPACK 1.0, DSTEDC (used in driver DSYEVD) was introduced in LAPACK 2.0, and DSTEGR (used in driver DSYEVR) was introduced in LAPACK 3.0. As can be seen, for large matrices DSTEGR is about 14 times faster than DSTEDC and nearly 50 times faster than DSTEQR.
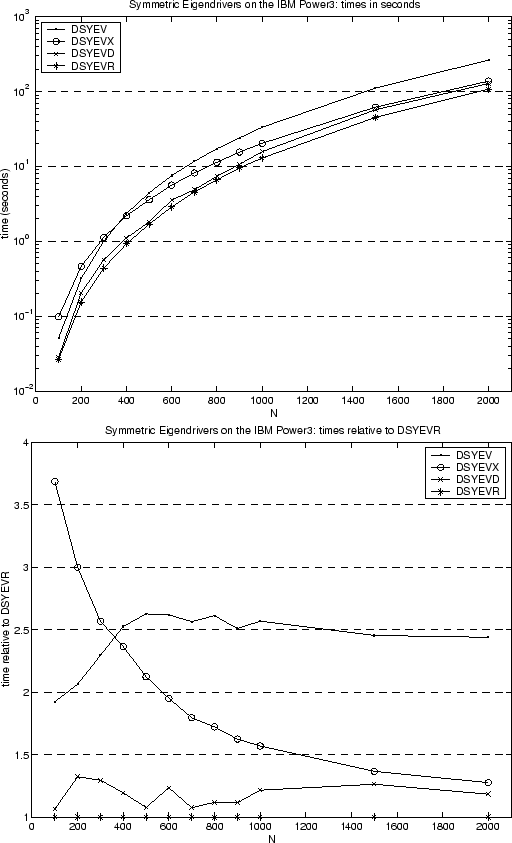
Next consider Figure 3.2, which compares the performance of four driver routines, DSYEV, DSYEVX, DSYEVD and DSYEVR, for computing all the eigenvalues and eigenvectors of a dense symmetric matrix. The times are shown on an IBM Power 3 for matrix dimensions from 100 to 2000. The symmetric matrix was chosen randomly. The cost of these drivers is essentially the cost of phases 1 and 3 (reduction to tridiagonal form and backtransformation) plus the cost of phase 2 (the symmetric tridiagonal eigenproblem) discussed in the last paragraph. Since the cost of phases 1 and 3 is large, performance differences in phase 2 are no longer as visible. We note that if we had chosen a test matrix with a large cluster of nearby eigenvalues, then the cost of DSYEVX would have been much larger, without significantly affecting the timings of the other drivers. DSYEVR is the driver of choice.
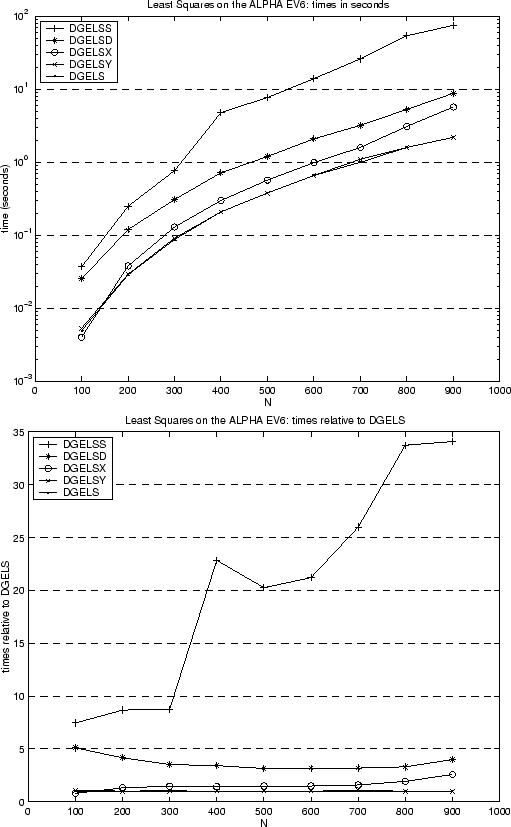
Finally consider Figure 3.3, which compares the performance of five drivers for the linear least squares problem, DGELS, DGELSY, DGELSX, DGELSD and DGELSS, which are shown in order of decreasing speed. DGELS is the fastest. DGELSY and DGELSX use QR with pivoting, and so handle rank-deficient problems more reliably than DGELS but can be more expensive. DGELSD and DGELSS use the SVD, and so are the most reliable (and expensive) ways to solve rank deficient least squares problems. DGELS, DGELSX and DGELSS were in LAPACK 1.0, and DGELSY and DGELSD were introduced in LAPACK 3.0. The times are shown on a Compaq AlphaServer DS-20 for squares matrices with dimensions from 100 to 1000, and for one right-hand-side. The matrices were chosen at random (which means they are full rank). First consider DGELSY, which is meant to replace DGELSX. We can see that the speed of DGELSY is nearly indistinguishable from the fastest routine DGELS, whereas DGELSX is over 2.5 times slower for large matrices. Next consider DGELSD, which is meant to replace DGELSS. It is 3 to 5 times slower than the fastest routine, DGELS, whereas its predecessor DGELSS was 7 to 34 times slower. Thus both DGELSD and DGELSY are significantly faster than their predecessors.
 |
 |
 |
| DGEMV | DGEMM | |||||||
| Values of n=m=k | ||||||||
| 100 | 1000 | 100 | 1000 | |||||
| Time | Mflops | Time | Mflops | Time | Mflops | Time | Mflops | |
| Dec Alpha Miata | .0151 | 66 | 27.778 | 36 | .0018 | 543 | 1.712 | 584 |
| Compaq AlphaServer DS-20 | .0027 | 376 | 8.929 | 112 | .0019 | 522 | 2.000 | 500 |
| IBM Power 3 | .0032 | 304 | 2.857 | 350 | .0018 | 567 | 1.385 | 722 |
| IBM PowerPC | .0435 | 23 | 40.000 | 25 | .0063 | 160 | 4.717 | 212 |
| Intel Pentium II | .0075 | 134 | 16.969 | 59 | .0031 | 320 | 3.003 | 333 |
| Intel Pentium III | .0071 | 141 | 14.925 | 67 | .0030 | 333 | 2.500 | 400 |
| SGI O2K (1 proc) | .0046 | 216 | 4.762 | 210 | .0018 | 563 | 1.801 | 555 |
| SGI O2K (4 proc) | 5.000 | 0.2 | 2.375 | 421 | .0250 | 40 | 0.517 | 1936 |
| Sun Ultra 2 (1 proc) | .0081 | 124 | 17.544 | 57 | .0033 | 302 | 3.484 | 287 |
| Sun Enterprise 450 (1 proc) | .0037 | 267 | 11.628 | 86 | .0021 | 474 | 1.898 | 527 |
megaflop SSYEV/DSYEV.
| Driver | Options | Operation |
| Count | ||
| xGESV | 1 right hand side | |
| xGEEV | eigenvalues only |
|
| xGEEV | eigenvalues and right eigenvectors |
|
| xGES{VD,DD} | singular values only |
|
| xGES{VD,DD} | singular values and left and right singular vectors |
|
| No. of | Values of n | |||||||
| proc. | nb | 100 | 1000 | |||||
| Time |
|
Mflops | Time |
|
Mflops | |||
| Dec Alpha Miata | 1 | 28 | .004 | 2.2 | 164 | 1.903 | 1.11 | 351 |
| Compaq AlphaServer DS-20 | 1 | 28 | .002 | 1.05 | 349 | 1.510 | 0.76 | 443 |
| IBM Power 3 | 1 | 32 | .003 | 1.67 | 245 | 1.210 | 0.87 | 552 |
| Intel Pentium II | 1 | 40 | .006 | 1.94 | 123 | 2.730 | 0.91 | 245 |
| Intel Pentium III | 1 | 40 | .005 | 1.67 | 136 | 2.270 | 0.91 | 294 |
| SGI Origin 2000 | 1 | 64 | .003 | 1.67 | 227 | 1.454 | 0.81 | 460 |
| SGI Origin 2000 | 4 | 64 | .004 | 0.16 | 178 | 1.204 | 2.33 | 555 |
| Sun Ultra 2 | 1 | 64 | .008 | 2.42 | 81 | 5.460 | 1.57 | 122 |
| Sun Enterprise 450 | 1 | 64 | .006 | 2.86 | 114 | 3.698 | 1.95 | 181 |
| No. of | Values of n | |||||||||
| proc. | nb | 100 | 1000 | |||||||
| True | Synth | True | Synth | |||||||
| Time |
|
Mflops | Mflops | Time |
|
Mflops | Mflops | |||
| Dec Alpha Miata | 1 | 28 | .157 | 87.22 | 70 | 64 | 116.480 | 68.04 | 81 | 86 |
| Compaq AS DS-20 | 1 | 28 | .044 | 23.16 | 423 | 228 | 52.932 | 26.47 | 177 | 189 |
| IBM Power 3 | 1 | 32 | .060 | 33.33 | 183 | 167 | 91.210 | 65.86 | 103 | 110 |
| Intel Pentium II | 1 | 40 | .100 | 32.26 | 110 | 100 | 107.940 | 35.94 | 87 | 93 |
| Intel Pentium III | 1 | 40 | .080 | 26.67 | 137 | 133 | 91.230 | 36.49 | 103 | 110 |
| SGI Origin 2000 | 1 | 64 | .074 | 41.11 | 148 | 135 | 54.852 | 30.46 | 172 | 182 |
| SGI Origin 2000 | 4 | 64 | .093 | 3.72 | 117 | 107 | 42.627 | 82.45 | 222 | 235 |
| Sun Ultra 2 | 1 | 64 | .258 | 78.18 | 43 | 38 | 246.151 | 70.65 | 38 | 41 |
| Sun Enterprise 450 | 1 | 64 | .178 | 84.76 | 62 | 56 | 163.141 | 85.95 | 57 | 61 |
| No. of | Values of n | |||||||||
| proc. | nb | 100 | 1000 | |||||||
| True | Synth | True | Synth | |||||||
| Time |
|
Mflops | Mflops | Time |
|
Mflops | Mflops | |||
| Dec Alpha Miata | 1 | 28 | .308 | 171.11 | 86 | 86 | 325.650 | 190.22 | 73 | 81 |
| Compaq AS DS-20 | 1 | 28 | .092 | 48.42 | 290 | 287 | 159.409 | 79.70 | 149 | 165 |
| IBM Power 3 | 1 | 32 | .130 | 72.22 | 204 | 203 | 230.650 | 166.53 | 103 | 114 |
| Intel Pentium II | 1 | 40 | .200 | 64.52 | 133 | 132 | 284.020 | 94.58 | 84 | 93 |
| Intel Pentium III | 1 | 40 | .170 | 56.67 | 156 | 155 | 239.070 | 95.63 | 100 | 110 |
| SGI Origin 2000 | 1 | 64 | .117 | 65.00 | 228 | 226 | 197.455 | 109.64 | 121 | 133 |
| SGI Origin 2000 | 4 | 64 | .159 | 6.36 | 167 | 166 | 146.975 | 284.28 | 164 | 179 |
| Sun Ultra 2 | 1 | 64 | .460 | 139.39 | 58 | 58 | 601.732 | 172.71 | 39 | 44 |
| Sun Enterprise 450 | 1 | 64 | .311 | 148.10 | 85 | 85 | 418.011 | 220.24 | 57 | 63 |
| No. of | Values of n | |||||||||
| proc. | nb | 100 | 1000 | |||||||
| True | Synth | True | Synth | |||||||
| Time |
|
Mflops | Mflops | Time |
|
Mflops | Mflops | |||
| Dec Alpha Miata | 1 | 28 | .043 | 23.89 | 61 | 61 | 36.581 | 21.37 | 73 | 73 |
| Compaq AS DS-20 | 1 | 28 | .011 | 5.79 | 236 | 236 | 11.789 | 5.89 | 226 | 226 |
| IBM Power 3 | 1 | 32 | .020 | 11.11 | 133 | 133 | 8.090 | 5.84 | 330 | 330 |
| Intel Pentium II | 1 | 40 | .040 | 12.90 | 67 | 67 | 29.120 | 9.70 | 92 | 92 |
| Intel Pentium III | 1 | 40 | .030 | 10.00 | 89 | 89 | 25.830 | 10.33 | 103 | 103 |
| SGI Origin 2000 | 1 | 64 | .024 | 13.33 | 113 | 113 | 12.407 | 6.89 | 215 | 215 |
| SGI Origin 2000 | 4 | 64 | .058 | 2.32 | 46 | 46 | 4.926 | 9.53 | 541 | 541 |
| Sun Ultra 2 | 1 | 64 | .088 | 26.67 | 30 | 30 | 60.478 | 17.36 | 44 | 44 |
| Sun Enterprise 450 | 1 | 64 | .060 | 28.57 | 92 | 45 | 47.813 | 25.19 | 56 | 56 |
| No. of | Values of n | |||||||||
| proc. | nb | 100 | 1000 | |||||||
| True | Synth | True | Synth | |||||||
| Time |
|
Mflops | Mflops | Time |
|
Mflops | Mflops | |||
| Dec Alpha Miata | 1 | 28 | .222 | 123.33 | 77 | 30 | 320.985 | 187.49 | 48 | 21 |
| Compaq AS DS-20 | 1 | 28 | .053 | 27.89 | 326 | 126 | 142.843 | 71.42 | 107 | 47 |
| IBM Power 3 | 1 | 32 | .070 | 38.89 | 245 | 95 | 251.940 | 181.91 | 61 | 26 |
| Intel Pentium II | 1 | 40 | .150 | 48.39 | 114 | 44 | 282.550 | 94.09 | 54 | 24 |
| Intel Pentium III | 1 | 40 | .120 | 40.00 | 142 | 56 | 244.690 | 97.88 | 62 | 27 |
| SGI Origin 2000 | 1 | 64 | .074 | 41.11 | 232 | 90 | 176.134 | 97.80 | 87 | 38 |
| SGI Origin 2000 | 4 | 64 | .145 | 5.80 | 118 | 46 | 198.656 | 384.25 | 77 | 34 |
| Sun Ultra 2 | 1 | 64 | .277 | 83.94 | 62 | 24 | 570.290 | 163.69 | 27 | 12 |
| Sun Enterprise 450 | 1 | 64 | .181 | 86.19 | 95 | 37 | 402.456 | 212.04 | 38 | 17 |
| No. of | Values of n | |||||||||
| proc. | nb | 100 | 1000 | |||||||
| True | Synth | True | Synth | |||||||
| Time |
|
Mflops | Mflops | Time |
|
Mflops | Mflops | |||
| Dec Alpha Miata | 1 | 28 | .055 | 30.56 | 123 | 121 | 47.206 | 27.57 | 141 | 141 |
| Compaq AS DS-20 | 1 | 28 | .021 | 11.05 | 310 | 318 | 20.658 | 10.33 | 323 | 323 |
| IBM Power 3 | 1 | 32 | .025 | 13.89 | 268 | 267 | 15.230 | 11.00 | 438 | 438 |
| Intel Pentium II | 1 | 40 | .060 | 19.35 | 112 | 111 | 44.270 | 14.74 | 151 | 151 |
| Intel Pentium III | 1 | 40 | .050 | 16.67 | 134 | 133 | 38.930 | 15.57 | 171 | 171 |
| SGI Origin 2000 | 1 | 64 | .035 | 19.44 | 189 | 191 | 24.985 | 13.87 | 267 | 267 |
| SGI Origin 2000 | 4 | 64 | .091 | 3.64 | 73 | 73 | 8.779 | 16.89 | 759 | 760 |
| Sun Ultra 2 | 1 | 64 | .149 | 45.15 | 45 | 45 | 93.417 | 26.81 | 72 | 71 |
| Sun Enterprise 450 | 1 | 64 | .102 | 48.57 | 66 | 65 | 70.597 | 37.20 | 94 | 94 |