




Next: Relationship to Symmetric Lanczos.
Up: Golub-Kahan-Lanczos Method
Previous: Golub-Kahan-Lanczos Method
Contents
Index
Golub-Kahan-Lanczos Bidiagonalization Procedure.
As discussed in §6.2,
the first phase of a transformation method for the SVD
is to compute unitary matrices 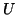 and
and 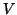 such that
such that
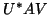 is in bidiagonal form. In fact, the first column
is in bidiagonal form. In fact, the first column 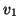 of
of 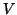 can be chosen as an arbitrary unit vector, after which
the other columns of
can be chosen as an arbitrary unit vector, after which
the other columns of 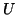 and
and 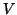 are generally determined uniquely.
We write this as
are generally determined uniquely.
We write this as
![\begin{displaymath}
U^{*} A V = B = \left[ \begin{array}{cccccc}
\alpha_1 & \be...
...\beta_{n-1} \\
& & & & &\alpha_{n} \\
\end{array} \right].
\end{displaymath}](img1761.png) |
(111) |
All 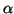 s and
s and 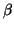 s are real even if
s are real even if 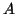 was complex.
was complex.
The constants 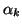 and
and 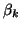 are given by
are given by
From the bidiagonal form (6.4) we may derive a double recursion
for the columns 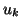 and
and 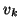 of
of 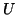 and
and 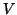 . Multiplying by
. Multiplying by 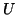 , we have
, we have
Equating the 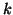 th columns on both sides, we get
th columns on both sides, we get
or
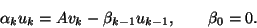 |
(112) |
On the other hand, from the relation
we get
or
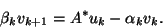 |
(113) |
Since the columns of 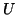 and
and 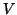 are normalized, we must have
are normalized, we must have
and
We summarize the recursion in the following algorithm.

Collecting the computed quantities from the first 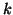 steps of the
algorithm, we have the following important relations:
steps of the
algorithm, we have the following important relations:
and
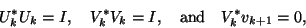 |
(116) |
where 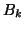 is the
is the 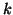 by
by 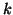 leading principal submatrix of
leading principal submatrix of 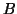 defined in (6.4).
defined in (6.4).





Next: Relationship to Symmetric Lanczos.
Up: Golub-Kahan-Lanczos Method
Previous: Golub-Kahan-Lanczos Method
Contents
Index
Susan Blackford
2000-11-20
![\begin{displaymath}
U^{*} A V = B = \left[ \begin{array}{cccccc}
\alpha_1 & \be...
...\beta_{n-1} \\
& & & & &\alpha_{n} \\
\end{array} \right].
\end{displaymath}](img1761.png)
![]() and
and ![]() are given by
are given by
![\begin{displaymath}
A
\left[\begin{array}{cccc}
v_1 & v_2 & \ldots & v_n
\e...
... & \beta_{n-1} \\
& & & & \alpha_n \\
\end{array} \right].
\end{displaymath}](img1766.png)
![\begin{displaymath}
A^{\ast} \left[\begin{array}{cccc}
u_1 & u_2 & \ldots & u_n...
... & \\
& & & \beta_{n-1} & \alpha_n \\
\end{array} \right],
\end{displaymath}](img1769.png)
![]() and
and ![]() are normalized, we must have
are normalized, we must have
![]() steps of the
algorithm, we have the following important relations:
steps of the
algorithm, we have the following important relations: