Cholesky Factorization



Next: Scalability
Up: Performance Results
Previous: QR Factorization
The PDSYRK routine performs rank-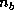 updates
on an
updates
on an  symmetric matrix
symmetric matrix 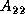 with an
with an
 column of blocks
column of blocks  .
After broadcasting
.
After broadcasting  rowwise and transposing it,
each process updates its local portion of
rowwise and transposing it,
each process updates its local portion of 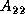 with its own copy
of
with its own copy
of  and
and  .
The update is complicated by the fact that the globally lower triangular
matrix
.
The update is complicated by the fact that the globally lower triangular
matrix 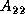 is not necessarily stored
in the lower triangular form in the local processes. For details
see [8].
The simplest way to do this is to repeatedly update one column of blocks
of
is not necessarily stored
in the lower triangular form in the local processes. For details
see [8].
The simplest way to do this is to repeatedly update one column of blocks
of 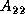 . However, if the block size is small,
this updating process will not be efficient.
It is more efficient to update several blocks of columns
at a time.
The PBLAS routine, PDSYRK efficiently updates
. However, if the block size is small,
this updating process will not be efficient.
It is more efficient to update several blocks of columns
at a time.
The PBLAS routine, PDSYRK efficiently updates 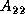 by combining
several blocks of columns at a time. For details, see [8].
by combining
several blocks of columns at a time. For details, see [8].

Figure 10: Performance of the Cholesky factorization on the Intel iPSC/860,
Delta, and Paragon.
The effect of the block size on the performance of the Cholesky factorization
is shown in Figure 9 on 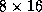 and
and 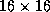 processors of the Intel Delta.
The best performance was obtained at the block size of
processors of the Intel Delta.
The best performance was obtained at the block size of  , but
relatively good performance could be expected with the block size of
, but
relatively good performance could be expected with the block size of
 , since the routine updates multiple column panels at a time.
, since the routine updates multiple column panels at a time.
Figure 10 shows the performance of the
Cholesky factorization routine.
The best performance was attained with the aspect ratio of  .
The routine ran at 1.8 Gflops for
.
The routine ran at 1.8 Gflops for  on the iPSC/860;
10.5 Gflops for
on the iPSC/860;
10.5 Gflops for 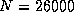 on the Delta; and
16.9 Gflops for
on the Delta; and
16.9 Gflops for 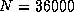 on the Paragon.
Since it requires fewer floating point operations (
on the Paragon.
Since it requires fewer floating point operations ( ) than
the other factorizations, it is not surprising
that its flop rate is relatively poor.
) than
the other factorizations, it is not surprising
that its flop rate is relatively poor.
If 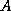 is not positive definite, the Cholesky factorization should be
terminated in the middle of the computation.
As outlined in Section 3.3,
a process
is not positive definite, the Cholesky factorization should be
terminated in the middle of the computation.
As outlined in Section 3.3,
a process  computes the Cholesky factor
computes the Cholesky factor  from
from 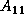 .
After computing
.
After computing  , process
, process  broadcasts a flag
to all other processes to stop the computation
if
broadcasts a flag
to all other processes to stop the computation
if 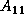 is not positive definite.
If
is not positive definite.
If 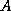 is guaranteed to be positive definite,
the process of broadcasting the flag can be skipped,
leading to a corresponding increase in performance.
is guaranteed to be positive definite,
the process of broadcasting the flag can be skipped,
leading to a corresponding increase in performance.



Next: Scalability
Up: Performance Results
Previous: QR Factorization
Susan Ostrouchov
Fri Apr 28 09:37:26 EDT 1995
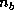 updates
on an
updates
on an  symmetric matrix
symmetric matrix 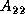 with an
with an
 column of blocks
column of blocks  .
After broadcasting
.
After broadcasting  rowwise and transposing it,
each process updates its local portion of
rowwise and transposing it,
each process updates its local portion of 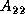 with its own copy
of
with its own copy
of  and
and  .
The update is complicated by the fact that the globally lower triangular
matrix
.
The update is complicated by the fact that the globally lower triangular
matrix 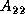 is not necessarily stored
in the lower triangular form in the local processes. For details
see [8].
The simplest way to do this is to repeatedly update one column of blocks
of
is not necessarily stored
in the lower triangular form in the local processes. For details
see [8].
The simplest way to do this is to repeatedly update one column of blocks
of 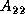 . However, if the block size is small,
this updating process will not be efficient.
It is more efficient to update several blocks of columns
at a time.
The PBLAS routine, PDSYRK efficiently updates
. However, if the block size is small,
this updating process will not be efficient.
It is more efficient to update several blocks of columns
at a time.
The PBLAS routine, PDSYRK efficiently updates 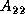 by combining
several blocks of columns at a time. For details, see [8].
by combining
several blocks of columns at a time. For details, see [8].

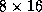 and
and 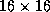 processors of the Intel Delta.
The best performance was obtained at the block size of
processors of the Intel Delta.
The best performance was obtained at the block size of  , but
relatively good performance could be expected with the block size of
, but
relatively good performance could be expected with the block size of
 , since the routine updates multiple column panels at a time.
, since the routine updates multiple column panels at a time.
 .
The routine ran at 1.8 Gflops for
.
The routine ran at 1.8 Gflops for  on the iPSC/860;
10.5 Gflops for
on the iPSC/860;
10.5 Gflops for 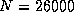 on the Delta; and
16.9 Gflops for
on the Delta; and
16.9 Gflops for 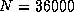 on the Paragon.
Since it requires fewer floating point operations (
on the Paragon.
Since it requires fewer floating point operations ( ) than
the other factorizations, it is not surprising
that its flop rate is relatively poor.
) than
the other factorizations, it is not surprising
that its flop rate is relatively poor.
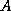 is not positive definite, the Cholesky factorization should be
terminated in the middle of the computation.
As outlined in Section
is not positive definite, the Cholesky factorization should be
terminated in the middle of the computation.
As outlined in Section  computes the Cholesky factor
computes the Cholesky factor  from
from 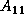 .
After computing
.
After computing