Figure 6: Performance of the LU factorization on the Intel iPSC/860,
Delta, and Paragon.
Figure 6 shows the performance of the
ScaLAPACK LU factorization routine on the Intel iPSC/860, the Delta,
and the Paragon in Gflops (gigaflops or a billion floating point
operations per second)
as a function of the number of processes.
The selected block size on the iPSC/860 and the Paragon was 
,
and on the Delta was 
,
and the best performance was attained with a process aspect ratio,
.
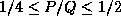The LU routine attained 2.4 Gflops for a matrix size of
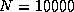on the iPSC/860; 12.0 Gflops for 
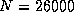on the Delta;
and 18.8 Gflops for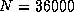 
on the Paragon.
The LU factorization routine requires pivoting for numerical stability. Many different implementations of pivoting are possible. In the paragraphs below, we outline our implementation and some optimizations which we chose not to use in order to maintain modularity and clarity in the library.
In the unblocked LU factorization routine (PDGETF2),
after finding the maximum value of the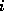 
-th column (PDAMAX),
the 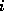-th row will be exchanged with the pivot row
containing the maximum value. Then the new 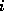-th row is
broadcast columnwise (
elements) in PDGER.
A slightly faster code may be obtained by combining the communications
of PDLASWP and PDGER.
That is, the pivot row is directly broadcast
to other processes in the grid column,
and the pivot row is replaced with the 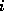-th row later.
The processes apply row interchanges (PDLASWP) to the left and
the right of the column panel of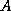 
(i.e., 
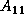and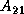 
).
These two row interchanges involve separate communications,
which can be combined.
Finally, after completing the factorization of the column panel
(PDGETF2),
the column of processes, which has the column panel,
broadcasts rowwise
the pivot information for PDLASWP, 
for PDTRSM,
and 
for PDGEMM.
It is possible to combine the three messages to save the number of
communications (or combine and ), and broadcast rowwise
the combined message.
Notice that a non-negligible time is spent broadcasting the column panel of
across the process grid.
It is possible to increase the overlap of communication to
computation by broadcasting each column rowwise
as soon as they are evaluated, rather than broadcasting
all of the panel across after factoring it.
With these modified communication schemes, the performance
of the routine may be increased, but in our experiments we have found
the improvement to be less than 5 % and, therefore, not worth the loss
of modularity.