Blocking Examples

 

Our first example is an algorithm that uses plane rotations for the QR factorization of real matrix X. In the description of these example algorithms we suppress all irrelevant detail. To that end, we use the notation f(x, y, z) to mean a generic function of the arguments x, y, and z which may be a different function at every occurrence.

 mmmmmmmmmmmmmmmm¯

   		for k = 1 to n do  

   				 for i = m to k+1 step -1 do  

(1)						 (c, s) = f(x(i,k), x(i-1,k));

   						 for j = k+1 to n do  

(2)								  ; od

   						 od 

   				 od 

There are two distinct true dependences here. Statement (2) at iteration (i,j,k) depends on statement (2) at iterations (i+1, j, k) (because x(i,j) is changed there) (i-1, j, k-1) (because x(i-1,j) is changed there). Each iteration (i,j,k) of statment (2) depends on statement (1) at iteration (i,k), so that is a column of C. Furthermore, statement (1) depends on statement (2) at iterations (i, k, k-1) and (i-1,k,k-1). Therefore, through the uses of c and s, statement (2) depends on itself at iterations (i,k,k-1) and (i-1,k,k-1); this dependence is weaker that a dependence on iteration (i, j-1, k-1) and (i-1,j-1,k-1), so if we take these to be the actual dependences we are going to be safe. There are also antidependences and output dependences, but these can be ignored for the moment. Thus,

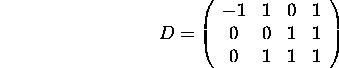
and

In this case, there are only three rays of the cone, namely,

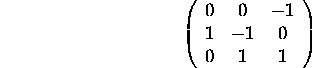
After improvement we arrive at the basis

Thus, the new indices are j, k, and k-i.

After replacing the index i by we have the following program:

 mmmmmmmmmmmmmmmm¯

   		for k = 1 to n do  

   				 for r = k-m to -1 do  

   						 (c(r,k), s(r,k)) = f(x(k-r,k), x(k-r-1,k));

   						 for j = k+1 to n do  

   								  ; od

   						 od 

   				 od 

Strip mining produces

 mmmmmmmmmmmmmmmm¯

   for k0 = 1 to n step b do  

   		 for k = k0 to  do 

   				 for r0 = k0-m to -1 step b do  

   						 for  to  do 

   								 (c(r,k), s(r,k)) = f(x(k-r,k), x(k-r-1,k));

   								 for j0 = k0+1 to n step b do  

   										 for  to  do  

   												  ; od

   										 od 

   								 od 

   						 od 

   				 od 

   		od 

Then loop interchanging produces

 mmmmmmmmmmmmmmmm¯

   for k0 = 1 to n step b do  

   		 for r0 = k0-m to -1 step b do  

   				 for j0 = k0 to n step b do  

   						 for k = k0 to  do 

   								 for  to  do 

   										 if j0 = k0 then (c(r,k), s(r,k)) = f(x(k-r,k), x(k-r-1,k)); 

   										 for  to  do  

   												  ; od

   										 od 

   								 od 

   						 od 

   				 od 

   		od 

  
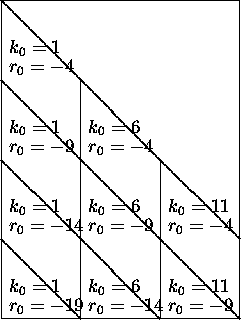
Figure 6: Blocking of the QR factorization of an matrix with .

This rather complicated blocked algorithm works as follows. We illustrate with m = 20, n = 15, b = (5, 5, 5). Elements of X are eliminated by plane rotations in patches, as shown in Figure 6. The values of k0 and r0 at which elements are eliminated is shown in each patch. The rotations used to do the elimination are applied only to columns in the current patch (during the block operation with j0 = k0). These rotations are stored and later applied to columns to the right of the patch (when j0 > k0).

For another example, consider the following program for the QR factorization which uses Householder transforms rather than plane rotations. In this pseudo-code we use the notation x(k:m,j) to refer to the vector of elements . We include it as an example of a program that can be blocked without using linear loop index transformation.

 mmmmmmmmmmmmmmmm¯

for k = 1 to n do  

		 ;

		 x(k,k) = f(x(k,k),s(k));

		 for j=k+1 to n step 

 do  

				   ;

				   x(k:m,j) = x(k:m, j) + s'(k,j) * x(k:m,k); od

		 od 

In Fortran, loops would be triply nested. The compiler, on detecting a dependence of some subsequent statement on the whole of an inner loop implementing a reduction operation, such as the norm and the inner product in the example, should choose to view those loops as atomic and therefore work with an index space of reduced dimension.

The dependences in (j,k) space are

The basis chosen is the obvious one: A = I. Thus, no skewing is done.

Now, we choose the order of the block loops. The measure of data flux given in Section 5 is the same for and for ; so neither order is preferred.

Note, however, that the two dependences are different in character. The dependence is a true dependence at every point of the index space. The other, expresses the dependence of iteration (j,k) on ``iteration'' (k,k) (the task performed outside the inner loop for given k); the data that are required are used in common by all the iterations with fixed k. Thus, for the purpose of determining data flux, this dependence direction should be given weight 1 (as are columns of C), not 2. If we make this change, the flux is greater for , so we make the k block loop innermost. This procedure yields a left-looking method in which all groups of Householder transforms are applied to a block of columns just before that block is triangularized. This allows the block to be held in local memory during the application of these transforms.

Acknowledgement We would like to thank Ilse Ipsen for her help at the beginning of our work on this problem and Mike Wolfe for his at the end.

Appendix. Proof of Lemma 3.

Let the matrices and . The face is subtended by the columns of . Let the matrix be factored
 
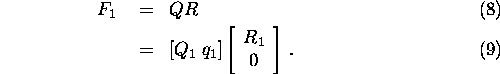
where Q is an orthogonal matrix, R is an upper triangular matrix, is , and is ; thus , and is a unit vector in the direction normal to the range of , which is the span of . The matrix is the orthogonal projector on . The factorization (9) always exists and is unique up to signs on the diagonal of R [10].

The columns of are the coordinates of the columns of with respect to the orthonormal basis (for the subspace of in which lies) consisting of the columns of . Thus

We must therefore show that .

From the identity it follows that ; thus

The proof is complete if we can show that . But since ,

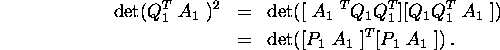
The result now follows from Lemma 1.